Для описания законов функционирования цифровых схем используется алгебра логики или булева алгебра. В основу алгебры логики положено понятие «событие», которое может наступить, либо не наступить. Наступившее событие считается истинным и выражается уровнем логической «1», не наступившее событие считается ложным и выражается уровнем логического «0».
На событие влияют переменные, причем влияют по определенному закону. Этот закон называется логической функцией, а переменные – аргументами. Т.о. логической функцией является функция у = f(x1, x2,… xn), принимающая значения «0» либо «1». Переменные x1, x2,… xn также имеют значения «0» либо «1».
Алгебра логики — раздел математической логики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов. В формулах алгебры логики переменные являются логическими или двоичными, т. е. принимающими только два значения — ложь и истина, которые обозначаются соответственно 0 и 1. Любая программа для ЭВМ содержит логические операции.
Устройства, предназначенные для формирования функций алгебры логики, называются логическими устройствами. Логическое устройство имеет сколь угодное количество входов и только один выход (рис. 1).
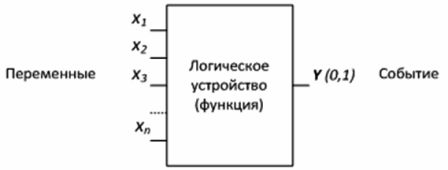
Рисунок 1 – Логическое устройство
Например, в состав электронного кодового замка входит логическое устройство, для которого событие (y) – это открытие замка. Для того чтобы событие произошло (y=1), т.е. замок открылся, необходимо определить переменные – десять кнопок кодонабирателя с цифрами. Определенные кнопки должны быть нажаты, т.е. принять значение «1» и при этом нажаты в определенной последовательности – логическая функция.
Любую логическую функцию удобно представить в виде таблицы состояний (таблицы истинности), где записываются возможные комбинации переменных (аргументов) и соответствующее им значение функции.
Логические устройства строятся на логических элементах, которые реализуют определённую функцию. Базовыми логическими функциями являются логическое сложение, логическое умножение и логическое отрицание.
1) ИЛИ (OR) - логическое сложение или дизъюнкция (от англ. disjunction - разъединение) - на выходе этого элемента появится логическая единица тогда, когда хотя бы на одном из входов появится единица. Логический ноль на выходе будет только тогда, когда на всех входах будет сигнал логического нуля.
Эту операцию можно реализовать с помощью контактной цепи с двумя параллельно включенными контактами. «1» на выходе такой цепи появится в том случае, если хотя бы один из контактов замкнут.
2) И (AND) - логическое умножение или конъюнкция (от англ. conjunction — соединение, & - амперсанд) - на выходе этого элемента сигнал логической единицы появляется только тогда, когда на всех входах будет присутствовать логическая единица. Если хотя бы на одном входе будет ноль, то и на выходе тоже будет ноль.
Эта операция может быть реализована контактной цепью, состоящей из последовательно включённых контактов.
3) НЕ (NOT) - логическое отрицание или инверсия, обозначается черточкой над переменной - операция выполняется над одной переменной x и значение у противоположно этой переменной.
Операция НЕ может быть осуществлена с помощью нормально замкнутого контакта электромагнитного реле: нет напряжения на обмотке реле (x = 0) – контакт замкнут и на выходе «1» (у = 1). При наличии напряжения на обмотке реле (х = 1) контакт разомкнут и на выходе «0» (у = 0).
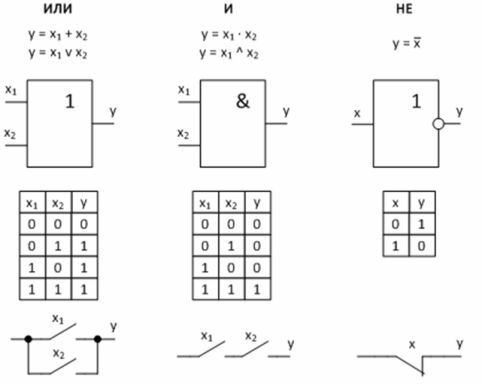
Рисунок 2 – Базовые логические функции и их реализация
В логических устройствах используются различные логические элементы. Особое значение имеют две универсальные логические операции, каждая из которых способна самостоятельно образовать любую логическую функцию.
4) И-НЕ - функция Шеффера.
5) ИЛИ-НЕ - функция Пирса.
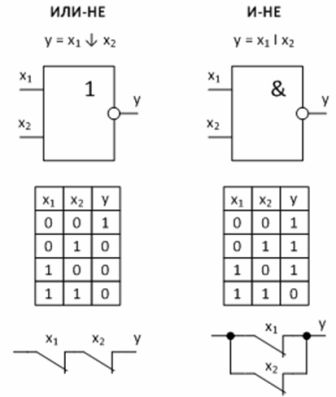
Рисунок 3 – Универсальные логические функции и их реализация
Пример: Схема охранной сигнализации на логических элементах. Генератор Г вырабатывает сигнал сирены, подавая его на усилительный каскад через логический элемент «И» на микросхеме DD2. При замкнутых состояниях охранных ключей S1 – S4 на входах элемента DD1 действует уровень «0» - на нижнем входе элемента «И» DD2 уровень «0», значит на затворе транзистора VT также «0».
В случае размыкания хотя бы одного из ключа, например S1, на вход элемента DD1 через резистор R1 поступит напряжение уровня «1», что приведёт к появлению «1» на втором входе элемента «И» DD1. Это позволит сигналу с генератора Г поступать на затвор транзистора, в нагрузке которого стоит динамик.
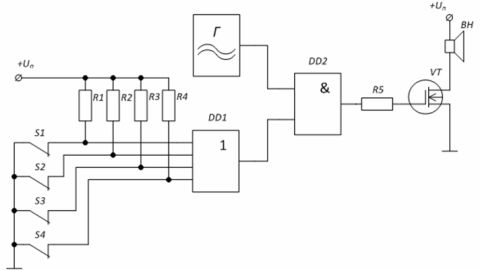
Рисунок 4 – Схема охранной сигнализации
Сложные цифровые схемы строятся путем многократного повторения базовых логических схем. Инструментом такого построения служит булева алгебра, которая применительно к цифровой технике называется алгеброй логики. В отличие от переменной в обычной алгебре логическая переменная имеет только два значения, которые называются логическим нулем и логической единицей.
Логический нуль и логическая единица обозначаются соответственно 0 и 1. В алгебре логики 0 и 1 не числа, а логические переменные. В алгебре логики существуют три основных операции между логическими переменными: логическое умножение (конъюнкция), логическое сложение (дизъюнкция) и логическое отрицание (инверсия).
Электронные схемы, выполняющие одну и ту же логическую функцию, но собранные на различных элементах, отличаются по потребляемой мощности, напряжению питания, значениям высокого и низкого уровней выходного напряжения, времени задержки распространения сигнала и нагрузочной способности.
Смотрите также по этой теме: Логические элементы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и их таблицы истинности