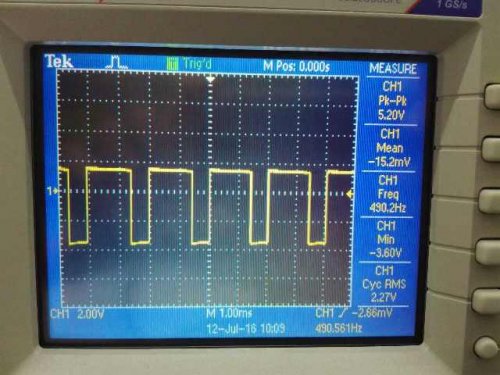
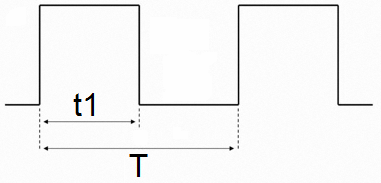
Одной из важнейших величин в импульсной технике является скважность S. Скважность S характеризует прямоугольный импульс, и определяет то, во сколько раз период импульса T больше его длительности t1. Так, меандр, например, имеет скважность равную 2, поскольку длительность импульса в такой последовательности равна половине его периода: S=T/t1=2.
Как видим, и в числителе, и в знаменателе стоят продолжительности, измеряемые в секундах, поэтому скважность — величина безразмерная. Для справки напомним, что меандр — это такая импульсная последовательность, где длительность положительной части импульса t1 равна длительности его исходного состояния t0.
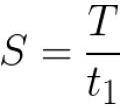
Величина обратная скважности называется коэффициентом заполнения D. Таким образом, теоретически скважность может изменяться от бесконечности до 1, тогда как соответствующий ей коэффициент заполнения может принимать значения от 0 до 1. Записывать величину скважности часто более удобно, чем коэффициент заполнения в виде дроби.
Например: D=0.5 – коэффициент заполнения меандра, или скважность S=2 – более удобочитаемая запись того же самого. Скважность S=10 соответствует коэффициенту заполнения D=0.1 — имеется ввиду, что продолжительность импульса в 10 раз меньше его периода (суммы его положительной и исходной частей).
Когда заходит речь о широтно-импульсной модуляции (ШИМ), то говорят, что при в драйвере происходит изменение ширины или длительности импульса, практически имеется ввиду изменение скважности при постоянной частоте. В этом контексте чем больше скважность — тем уже импульс, чем меньше скважность — тем шире импульс.
Здесь и просматривается этимологическая связь с русским словом «скважина»: большая скважина (по сути - яма между импульсами в последовательности) — сам импульс выглядит как более узкий, маленькая скважина — импульсы широкие (а вот яма между ними - узкая).
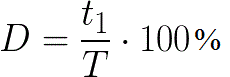
В англоязычной литературе не используется термин «скважность», а используется лишь термин «duty cycle» - рабочий цикл, являющийся аналогом русскоязычного термина «коэффициент заполнения» (D), только указывается он обычно не дробью, а в процентах. Например, мы пишем D=0.5, а в англоязычной литературе можно встретить 50% duty cycle или D = 50%, когда речь идет о меандре. Или D = 30% если длительность импульса соотносится с его периодом как 30 к 100.
Давайте рассмотрим простой практический пример. Лампочка включается на одну секунду через каждые 59 секунд, затем на 59 секунд гаснет, и так все время повторяется в течение неопределенного времени.
Что это значит? Длительность импульса t1 = 1 секунда, период импульса T = 59+1 = 60 секунд. Следовательно с какой скважностью включается лампочка?
Со скважностью S = 60/1. Скважность 60. Значит коэффициент заполнения равен 1/60, то есть D = 0,01666 или duty cycle 1,66%. В данном примере отчетливо видно, что запись в терминах скважности S = 60 более удобочитаема и точна, чем запись в форме коэффициента заполнения D = 0,01666 или duty cycle 1,666%.
Наконец, еще одно полезное применение скважности. Счетчики-дешифраторы импульсов (типа К561ИЕ8) способны делить импульсную последовательность на отдельные импульсы, здесь снова значение скважности подходит лучше, оно может быть определено через разрядность счетчика и сосчитано (пропорционально количеству импульсов, подсчитанных счетчиком).
Таким образом, даже для цифровой техники оперирование напрямую скважностью импульсов часто оказывается более удобным, чем свойственным принятому в англоязычной литературе коэффициентом заполнения.
Андрей Повный