Поскольку в современных электрических, особенно в промышленных, сетях неизменно присутствуют нелинейные элементы, то как следствие кривые тока и кривые напряжения искажаются, в сетях появляются высшие гармоники.
Высшие гармонические в кривых тока и напряжения возникают при наличии в сети устройств с нелинейными характеристиками (выпрямителей, трансформаторов, генераторов и др.). Если кривые напряжения трех фаз искажены, но во всех трех фазах одинаково, то и высшие гармонические во всех трех фазах по амплитуде одинаковы. То же справедливо и для высших гармонических тока.
В первую очередь несинусоидальность обусловлена наличием статических преобразователей, далее — синхронными генераторами, сварочными аппаратами, флюоресцентными лампами, дуговыми печами, трансформаторами, двигателями и другими нелинейными нагрузками.
Математически несинусоидальность кривых тока и напряжения можно представить как сумму главной гармоники сетевой частоты и ее гармоник более высокого порядка, ей кратных. Гармонический анализ в результате приводит к тригонометрическому ряду Фурье, и значения частот и фаз возникающих гармоник могут быть легко рассчитаны по формуле:
Фактически итоговое сочетание несинусоидальных напряжений и токов в трехфазной сети может быть несимметричным или симметричным. Симметричная система несинусоидальных напряжений для кратных трем гармоник (k = 3n) приводит к образованию системы напряжений нулевой последовательности.
Далее, при k = 3n+1, гармоника в трехфазной сети порождает симметричную систему напряжений обратной последовательности. Так, каждая k-гармоника симметричной системы несинусоидальных напряжений дает в итоге симметричную систему фазных напряжений прямой, обратной либо нулевой последовательностей.
Однако практически система фазных несинусоидальных напряжений оказывается несимметричной. Так, магнитопроводы трехфазных трансформаторов сами по себе являются и нелинейными, и несимметричными, поскольку длины магнитных путей для средних и крайних фаз имеют различие в 1,9 раз. Как следствие действующие значения токов намагничивания средней фазы в 1,3 — 1,55 раз меньше чем значения токов намагничивания для крайних фаз.
Несимметричные гармоники раскладываются на симметричные составляющие, когда любая k-гармоника образует несимметричную систему фазных напряжений, и в типичных случаях содержит в себе компоненты трех последовательностей — нулевой, прямой и обратной.
Трехфазным сетям с изолированной нейтралью свойственно отсутствие в каждой из фаз составляющих нулевой последовательности при условии, что нет замыканий на землю. В итоге в фазных токах нет кратных трем гармоник, а есть остальные гармоники, которые содержат в себе компоненты обратной и прямой последовательности.
Мощные выпрямители, как правило, на стороне постоянного тока имеют большие индуктивности, коими являются обмотки машин постоянного тока и сглаживающие реакторы. Индуктивности эти многократно превышают эквивалентную индуктивность стороны переменного тока, поэтому такие выпрямители по отношению к питающей сети переменного тока ведут себя как источники тока высших гармоник. Направляемый в сеть ток на частоте гармоники имеет величину, не зависящую от параметров питающей сети.
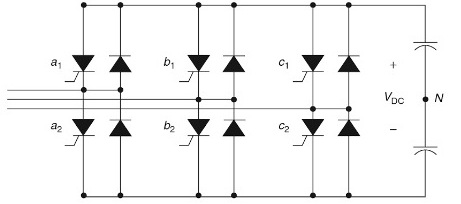
Для трехфазных электрических сетей характерно использование в качестве таких преобразователей трехфазные двухполупериодные выпрямители на 6 вентилей, от того они и называются шестипульсными или шестифазными. Кривую тока для каждой из фаз в этом случае можно описать уравнением (для тока одной фазы А):
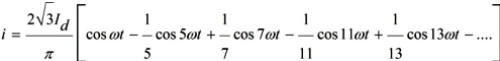
Видно, что фазные токи содержат лишь нечетные гармоники не кратные трем, и знаки этих гармоник чередуются: положительные гармоники 6k+1-порядка и отрицательные 6k-1-порядка.
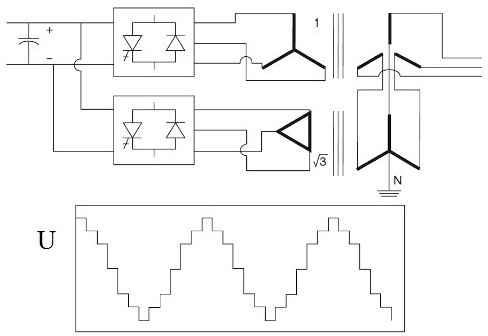
Если применяется выпрямитель двенадцатифазный, когда пара шестифазных выпрямителей подключается к паре трехфазных трансформаторов (вторичные напряжения сдвинуты между собой по фазе на пи/6), то проявятся гармоники соответственно 12k+1 и 12k-1-порядков.
До того как стали применяться выпрямители, главным источником высших гармоник в электрических сетях являлись лишь трансформаторы и различные электрические машины. Но и сегодня трансформаторы оказываются наиболее распространенными элементами электрических сетей.
Причина, по которой трансформаторы генерируют высшие гармоники — это нелинейная кривая намагничивания магнитопроводов и неизменное присутствие петли гистерезиса. Нелинейная кривая намагничивания и петля гистерезиса порождают искажения исходного синусоидального тока намагничивания холостого хода, и следствием становятся высшие гармоники в токе, который трансформатор потребляет от сети.
Трансформаторы класса 110 кВ имеют холостой ток не более 1%, а трансформаторы класса 6-10 кВ — не более 2-3%. Это малые токи, и активные потери от них в магнитопроводе незначительны. Здесь имеет значение кривая намагничивания, а не петля гистерезиса.
Кривая намагничивания симметрична, и при разложении в ряд Фурье четные гармоники отсутствуют. Искажение тока намагничивания вызывается нечетными гармониками, среди которых и кратные трем. Третья гармоника особенно сильно выражена, но наиболее существенными оказываются также и 5 и 7 гармоники.
Гармоники ЭДС и гармоники тока свойственны и двигателям, как синхронным, так и асинхронным. Данные гармоники обуславливаются теми же явлениями, что и гармоники тока, порождаемые трансформаторами — нелинейность кривой намагничивания материалов, из которых изготовлены статор и ротор.
Частотный спектр гармоник тока электродвигателей, так же как и у трансформаторов, включает в себя нечетные гармоники, среди которых, очевидно, и кратные трем. Наиболее существенны здесь 3, 5 и 7 гармоники.
Как и в случае с трансформаторами, приближенные расчеты позволяют принять в процентном отношении содержание токов 3, 5 и 7 гармоник на уровне 40% - для третьей гармоники, 30% - для пятой гармоники, и 20% - для седьмой гармоники (проценты от тока холостого хода).