В этой статье выясним, каковы должны быть соотношения параметров источника и приемника для того, чтобы добиться оптимального режима работы электрической цепи. Энергетические соотношения важны также и для техники слабых токов. В принципе эти вопросы можно рассмотреть на примере простейшей электрической цепи.
Цепь состоит из источника постоянного тока с ЭДС Е и внутренним сопротивлением Rвт, который вырабатывает электрическую энергию, и получающего энергию приемника с сопротивлением нагрузки Rн.
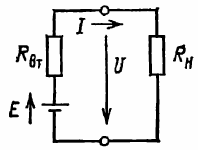
Рис. 1. Схема для пояснения соотношения мощностей в простейшей цепи
Так как источник имеет внутреннее сопротивление, то часть развиваемой им электрической энергии преобразуется в тепловую в нем самом.
Ток в цепи, изображенной на рис. 1
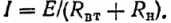
На основании этого уравнения определим мощность приемника (мощность преобразования электрической энергии в другие виды):
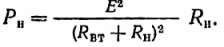
Аналогично мощность потерь в источнике:
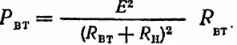
Электрическая мощность источника должна быть равна сумме мощностей, преобразуемых в другие виды в источнике и приемнике, т. е. должен существовать баланс мощностей (как и для любых цепей):
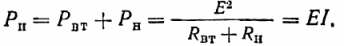
В выражение для мощности Рн может быть также введено и напряжение на выводах U.
Мощность приемника:
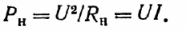
Коэффициент полезного действия (КПД), определяемый как отношение мощности приемника (полезной) к развиваемой мощности:
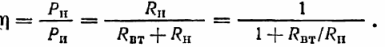
Уравнение показывает, что КПД зависит от соотношения сопротивления нагрузки и внутреннего сопротивления. Значения этих сопротивлений являются определяющим фактором в распределении мощности, развиваемой источником:
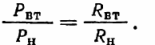
Мощность Рн следует рассматривать как полезную, мощность потерь в источнике Рвт определяет только нагрев источника, и, следовательно, соответствующая энергия расходуется непродуктивно.
КПД растет с увеличением отношения Рн/Рвт.
Для того чтобы получить большое значение КПД следует выполнять соотношение Рн > Рвт, т. е. электрическая цепь должна работать в режиме, близком к режиму холостого хода источника.
На практике для соотношения мощностей могут быть поставлены два различных требования: большое значение КПД и наличие согласования по мощности. Требование большого КПД выдвигается, например, тогда, когда нужно передать по проводам большое количество энергии или же преобразовать эту энергию в электрических машинах. Даже небольшое повышение значения КПД дает в таких случаях большую экономию.
Так как использование больших энергий характерно прежде всего для техники сильных токов, то, следовательно, в этой области следует работать в режимах, близких к режиму холостого хода. Кроме того, при работе в таких режимах напряжение на выводах лишь незначительно отличается от ЭДС источника.
В технике слабых токов (особенно в технике связи и измерительной технике) применяются очень маломощные источники, имеющие к тому же большие внутренние сопротивления. В таких случаях КПД, характеризующий процесс передачи энергии, часто имеет второстепенное значение, а на первый план выдвигается требование максимально возможного значения получаемой приемником мощности.
В то время, как в технике сильных токов бесполезные или даже вредные преобразования энергии — потери энергии снижаются при повышении КПД, в технике слабых токов эффективность использования установок и приборов повышается при правильном согласовании мощностей в электрических цепях.
Условие получения максимально возможной мощности приемника Рвmах от источника с данными ЭДС и внутренним сопротивлением:
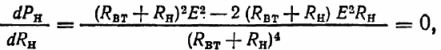
Откуда следует, что условие максимальной мощности приемника выполняется при соблюдении равенства Rн = Rвт.
Таким образом, при равенстве сопротивлений приемника и внутреннего сопротивления источника получаемая приемником мощность является максимальной.
Если Rн = Rвт, то
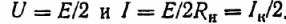
Для мощности, получаемой приемником, имеем:
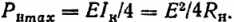
Пример. При помощи термоэлектрического преобразователя (термопары) с внутренним сопротивлением Rвт = 5 Ом можно получить напряжение 0,05 мВ/°С. Наибольшая разница температур 200 °С. Какие электрические данные должен иметь показывающий электрический прибор (сопротивление, мощность, ток), если он должен получить от преобразователя максимальную мощность.
Дать решение для двух случаев:
а) прибор подключен непосредственно к преобразователю;
б) прибор подключается при помощи двух медных проводов длиной l = 1000 м каждый с площадью поперечного сечения S = 1 мм2.
Решение. Максимальное напряжение на выводах термоэлектрического преобразователя равно его ЭДС Е = 200*0,05 = 10 мВ.
При этом показание включенного в цепь прибора должно быть максимальным (на верхнем пределе измерения).
а) Для того чтобы мощность прибора была максимальной, необходимо добиться согласования сопротивлений прибора и преобразователя. С этой целью выбираем сопротивление прибора Rн равным сопротивлению термоэлемента, т. е. Rн = Rт = 5 Ом.
Находим максимальную мощность прибора:
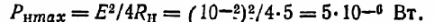
Определяем ток:
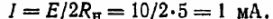
б) Если сопротивлением проводов нельзя пренебречь, то его следует учитывать при определении суммарного внутреннего сопротивления активного двухполюсника, состоящего из термоэлемента и двух проводов, так как в противном случае возникает рассогласование приемника и источника по мощности.
Найдем сопротивление проводов, имея в виду, что удельное сопротивление равно 0,0178 мкОм-м:
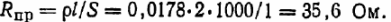
Таким образом, нужный уровень сопротивления прибора равен:
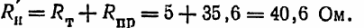
При таком значении внутреннего сопротивления мощность прибора будет максимальной
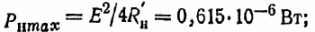
Ток в цепи:
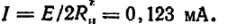
Полученные результаты показывают, что целесообразно выбирать источники с малым значением внутреннего сопротивления, а площадь поперечного сечения соединительных проводов должна быть достаточно большой.
Очень часто при проведении таких измерений расчет согласования приемника и источника сводится к тому, что из имеющихся приборов выбирается тот, у которого при заданном или известном максимальном значении измеряемой величины получается наибольшее отклонение стрелки и, следовательно, обеспечивается наибольшая точность отсчета по шкале.