Форму кривых напряжения и тока принято считать практически синусоидальной, если любая ее ордината отличается от соответствующей ординаты синусоиды, равной ей по амплитуде, на отрезок, не превосходящий 5 % амплитуды.
Синусоидальность может быть проверена несколькими способами. Используя наиболее простой из них, наблюдают исследуемую кривую на экране электронно-лучевого осциллографа.
Для этого предварительно наносят на экран прибора или на прозрачную пластину две одинаковые линии синусоидальной формы, сдвинутые по вертикали одна относительно другой на 10% их амплитуды (рис. 1).
Затем на вход Y осциллографа подают проверяемое напряжение и, регулируя усиление по каналу Y и период развертки, добиваются таких размеров кривой на экране, чтобы она располагалась внутри полосы, ограниченной вспомогательными синусоидами. Если это удается, то напряжение считают практически синусоидальным.
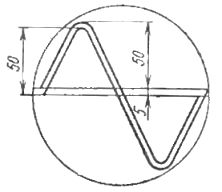
Рис. 1. Вспомогательные кривые для определения формы кривой тока и напряжения с помощью электронно-лучевого осциллографа
Чтобы рассмотреть второй способ определения синусоидальности кривой, введем несколько определений. Как известно, периодическая изменяющаяся величина может быть охарактеризована действующим, средним и максимальным (амплитудным) значениями. Если периодическая величина х изменяется по синусоидальному закону, то все ее значения связаны между собой определенным образом.
Например, отношение амплитудного значения к действующему, называемое коэффициентом амплитуды ka = xm/x = √2 = 1,41, отношение среднего значения за полупериод к амплитудному, называемое коэффициентом среднего значения kcр = xcp/xm = 2/π = 0,637, и, наконец, отношение действующего значения к среднему, называемое коэффициентом формы kф = x/xср = π/(2√2) = 1,11.
Ориентируясь на эти соотношения, стандарт допускает определять синусоидальность формы кривой периодической величины по результатам одновременного измерения среднего и действующего значений. Кривая считается практически синусоидальной если 1,132 > kф > 1,088.
В связи с тем что большинство используемых в практике испытаний измерительных приборов градуируется в действующих значениях, непосредственно измерять среднее и действующее значения не всегда представляется возможным. В этом случае исследуемую величину измеряют одновременно амплитудным (пиковым) и электродинамическим вольтметрами. При необходимости определения всех трех названных коэффициентов следует подключить выпрямительный вольтметр.
Показания вольтметров и коэффициенты, характеризующие синусоидальность формы связаны соотношениями: ka = 1,41U1/U2, kф = U2/0,9U3, kcp = 0,673 = U3/U1, где U1, U2, U3 — показания амплитудного, электродинамического и выпрямительного вольтметров по шкалам, проградуированным в действующих значениях синусоидального напряжения.
Пример. Для определения несинусоидальности формы кривой напряжения вторичной обмотки трансформатора фазное напряжение было одновременно измерено амплитудным В3-43, электродинамическим Д-556 и выпрямительным Ц4317 вольтметрами.
Их показания составили U1 = 76 В, U2 = 61 В, U3 = 59,5 В. Тогда ka = 1,41 х 76/61 = 1,76, kф = 1,11 х 61/59,5 = 1,14, kcp = 0,637 х 59,5/76 = 0,5
В связи с тем что для синусоидальной кривой эти коэффициенты должны быть равны 1,41, 1,11 и 0,637 соответственно, можно сделать вывод о том что напряжение на вторичной обмотке трансформатора имеет несинусоидальную форму. Обратим внимание на то, что при синусоидальном напряжении показания всех трех вольтметров должны быть равны.