Что такое контактная разность потенциалов

Если два образца, изготовленные из двух разных металлов, плотно прижать друг к другу, то между ними возникнет контактная разность потенциалов. Итальянский физик, химик и физиолог Алессандро Вольта обнаружил данный феномен в 1797 году, занимаясь изучением электрических свойств металлов.

Вольта установил тогда, что если соединить металлы в цепь в таком порядке: Al, Zn, Sn, Pb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd, то каждый следующий металл в полученной цепочке обретет потенциал ниже предыдущего.

Кроме того, ученый выяснил, что несколько металлов, объединенные таким способом, дадут одну и ту же разность потенциалов между концами образованной цепи, независимо от последовательности расположения данных металлов в этой цепи — это положение известно теперь как закон последовательных контактов Вольта.

Согласно этому закону, контактная разность потенциалов в цепи из нескольких металлов равна алгебраической сумме разностей потенциалов на каждом контакте, а в замкнутом кольце из металлов при одинаковой температуре и отсутствии химических реакций ЭДС (электродвижущая сила) равна нулю.

Такой закон основан на принципе сохранения энергии и указывает, что суммарная разность потенциалов зависит только от первого и последнего металла в цепи, а не от порядка их соединения.

Физически это объясняется тем, что электроны переходят из металла с более высоким уровнем Ферми (энергетическим уровнем электронов при 0 К) в металл с более низким уровнем Ферми, что вызывает перераспределение зарядов и создание потенциального барьера — контактной разности потенциалов.

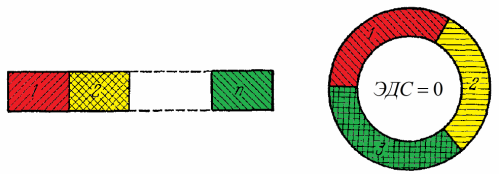
Здесь крайне важно понимать, что для точного выполнения закона последовательности контактов необходимо, чтобы вся цепочка металлов находилась при одной и той же температуре.

Если теперь данную цепь замкнуть концами саму на себя, то из закона будет следовать, что ЭДС в цепи окажется равна нулю. Но только при условии, что вся она (металл 1, металл2, металл3) находится при одной и той же температуре, иначе бы нарушился главный закон природы - закон сохранения энергии.

Для различных пар металлов контактная разность потенциалов будет своей определенной, из диапазона от десятых и сотых долей вольта до единиц вольт.

Чтобы понять причину появления контактной разности потенциалов, удобно воспользоваться моделью свободных электронов.

Пусть оба металла пары находятся при абсолютно нулевой температуре, тогда все уровни энергии, включая границу Ферми, окажутся заполнены электронами. Значение энергии (границы) Ферми связано с концентрацией электронов проводимости в металле следующим соотношением:

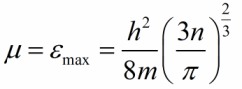
m - масса покоя электрона, h - постоянная Планка, n – концентрация электронов проводимости

Принимая во внимание данное соотношение, приведем в плотный контакт два металла с разными энергиями Ферми, и следовательно с разными концентрациями электронов проводимости.

Допустим для нашего примера, что второй металл имеет большую концентрацию электронов проводимости, и соответственно уровень Ферми у второго металла выше чем у первого.

Тогда при соприкосновении металлов друг с другом начнется диффузия (проникновение из одного металла — в другой) электронов из металла 2 — в металл 1, ведь в металле 2 есть заполненные энергетические уровни, которые находятся выше уровня Ферми первого металла, значит электроны с этих уровней станут заполнять в металле 1 свободные верхние уровни.

Обратное движение электронов в такой ситуации энергетически невозможно, ведь во втором металле все нижележащие уровни энергии уже полностью заполнены. В конце концов металл 2 зарядится положительно, а металл 1 — отрицательно, при этом уровень Ферми первого металла станет выше чем был, а у второго металла — снизится. Изменение это будет таковым:

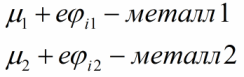
В результате между контактирующими металлами возникнет разность потенциалов, и соответствующее ей электрическое поле, которое теперь станет препятствовать дальнейшей диффузии электронов.

Ее процесс полностью остановится, когда разность потенциалов достигнет определенной величины, соответствующей равенству уровней Ферми двух металлов, при котором в металле 1 не останется свободных уровней для вновь поступающих электронов из металла 2, а в металле 2 так и не освободятся уровни для возможности миграции электронов из металла 1. Наступит энергетическое равновесие:

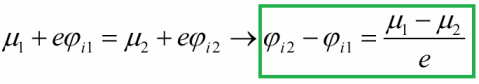
Поскольку заряд электрона отрицателен, то будем иметь следующее положение относительно потенциалов:

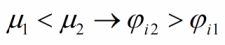
Хотя изначально мы и приняли температуру металлов равной абсолютному нулю, тем не менее аналогичным образом равновесие будет наступать при любой температуре.

Энергия Ферми при наличии электрического поля будет ни чем иным как химическим потенциалом единственного электрона в электронном газе, отнесенным к заряду этого самого единичного электрона, а так как в условиях равновесия химические потенциалы электронных газов обеих металлов будут равны, то стоит лишь добавить в рассмотрение зависимость химического потенциала от температуры.

Итак, рассмотренная нами разность потенциалов называется внутренней контактной разностью потенциалов и удовлетворяет закону последовательных контактов Вольта.

Давайте оценим данную разность потенциалов, для этого выразим энергии Ферми через концентрации электронов проводимости, после чего подставим численные значения констант:

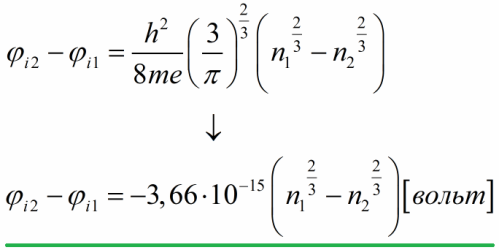
Таким образом, на базе модели свободных электронов, внутренняя контактная разность потенциалов для металлов имеет порядок величин от сотых долей вольта до единиц вольт. 

Такая разность обусловлена различием концентраций электронов проводимости и уровней Ферми в разных металлах, приводя к перераспределению зарядов на контакте и установлению равновесия, при котором электроны перестают диффундировать между металлами.

Контактная разность потенциалов зависит только от химического состава металлов и температуры их контакта, и в разомкнутой цепи она равна алгебраической сумме разностей потенциалов на каждом контакте.

Примеры контактных разностей потенциалов для металлов:

Популярные вопросы

Вопрос: Можно ли измерить контактную разность потенциалов обычным вольтметром?

Нет, и это принципиальный момент. На выводах прибора всегда образуются собственные контактные разности потенциалов между щупами и металлом, которые компенсируют измеряемую величину. Чтобы зафиксировать контактную разность потенциалов, используют методы, исключающие прямой контакт металлов с измерительными электродами.

Вопрос: Что происходит, если в паре металлов один заменить полупроводником?

У полупроводников концентрация носителей заряда намного ниже и сильно зависит от температуры, поэтому контактная разность потенциалов на границе металл-полупроводник значительно превышает аналогичную величину для пар из двух металлов. Именно это делает полупроводники основой термоэлектрических генераторов, где на один градус разности температур термо-ЭДС достигает долей вольта, тогда как у металлов она измеряется микровольтами.

Вопрос: Как контактная разность потенциалов связана с эффектом Зеебека?

Если два спая разнородных металлов находятся при одной температуре - суммарная ЭДС в замкнутой цепи равна нулю. Но стоит нагреть один спай, его контактная разность потенциалов изменится, потому что энергия Ферми зависит от температуры - и в цепи появляется ненулевая термо-ЭДС. Именно этот принцип лежит в основе термопары.

Вопрос: Что такое эффект Пельтье и какое отношение он имеет к контактным явлениям?

Эффект Пельтье - обратный к Зеебеку: если пропустить ток через контакт двух разнородных проводников, контакт будет либо нагреваться, либо охлаждаться в зависимости от направления тока. Физически это объясняется тем, что контактное поле либо помогает движению электронов, либо мешает ему, что выражается в поглощении или выделении тепла.

Вопрос: Есть ли практическое применение контактной разности потенциалов помимо термопар?

Да: на том же принципе работают термоэлектрические генераторы (ТЭГ), которые преобразуют промышленное отработанное тепло или тепло радиоизотопов в электроэнергию. Их применяют на космических аппаратах, газопроводах и в системах утилизации тепла двигателей, где нет смысла использовать турбину.

Вопрос: Что такое внешняя контактная разность потенциалов и чем она отличается от внутренней?

Внутренняя контактная разность потенциалов возникает непосредственно в тонком приконтактном слое и обусловлена выравниванием уровней Ферми. Внешняя связана с разницей работ выхода электронов из поверхности металлов в вакуум - она действует в пространстве над поверхностью металла и важна, например, при анализе эмиссии электронов.

Вопрос: Почему контактная разность потенциалов не запитает нагрузку без разности температур?

Потому что в замкнутой цепи из металлов при одинаковой температуре все контактные разности потенциалов компенсируют друг друга - суммарная ЭДС равна нулю. Это прямое следствие закона сохранения энергии: иначе металлическая петля стала бы вечным двигателем.

Вопрос: Влияет ли окисление поверхности металлов на контактную разность потенциалов?

Да, и существенно. Оксидная пленка изменяет работу выхода электронов и может создавать дополнительные барьеры на контакте. Именно поэтому в прецизионных термопарах и контактах важна чистота поверхности: загрязнения и оксиды вносят систематическую погрешность в измерения температуры.

Вопрос: Как контактные явления учитываются при монтаже электрических соединений?

На практике в сильноточных цепях разнородные металлы на контакте создают не только разность потенциалов, но и зону ускоренной электрохимической коррозии. Поэтому соединения алюминий-медь делают через специальные биметаллические наконечники или пасты, предотвращающие прямой контакт металлов и связанное с ним разрушение.

Вопрос: Существует ли аналог контактной разности потенциалов в полупроводниках?

Да - это встроенное электрическое поле p-n-перехода. Когда контактируют полупроводники с разными типами проводимости, носители заряда диффундируют через границу и создают барьерный слой с разностью потенциалов - по той же физической причине, что и в металлах, только выраженной значительно сильнее из-за малой концентрации носителей.

Андрей Повный