На практике нередко приходится рассчитывать сопротивление различных проводов. Это можно сделать с помощью формул или по данным, приведенным в табл. 1.
Влияние материала проводника учитывается с помощью удельного сопротивления, обозначаемого греческой буквой ? и представляющего собой сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Наименьшим удельным сопротивлением ? = 0,016 Ом•мм2/м обладает серебро. Приведем среднее значение удельного сопротивления некоторых проводников:
Серебро - 0,016, Свинец - 0,21, Медь - 0,017, Никелин - 0,42, Алюминий - 0,026, Манганин - 0,42, Вольфрам - 0,055, Константан - 0,5, Цинк - 0,06, Ртуть - 0,96, Латунь - 0,07, Нихром - 1,05, Сталь - 0,1, Фехраль -1,2, Бронза фосфористая - 0,11, Хромаль - 1,45.При различных количествах примесей и при разном соотношении компонентов, входящих в состав реостатных сплавов, удельное сопротивление может несколько измениться.
Сопротивление рассчитывается по формуле:
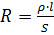
где R — сопротивление, Ом; удельное сопротивление, (Ом•мм2)/м; l — длина провода, м; s — площадь сечения провода, мм2.
Если известен диаметр провода d, то площадь его сечения равна:
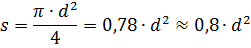
Измерить диаметр провода лучше всего с помощью микрометра, но если его нет, то следует намотать плотно 10 или 20 витков провода на карандаш и измерить линейкой длину намотки. Разделив длину намотки на число витков, найдем диаметр провода.
Для определения длины провода известного диаметра из данного материала, необходимой для получения нужного сопротивления, пользуются формулой
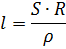
Таблица 1.
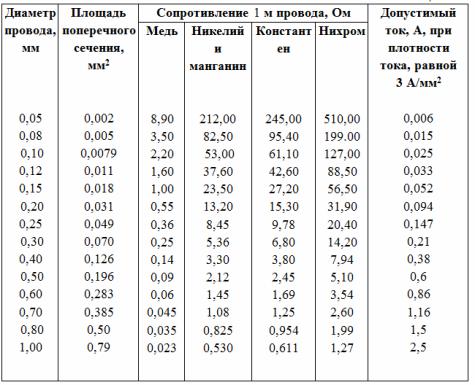
Примечание. 1. Данные для проводов, не указанных в таблице, надо брать как некоторые средние значения. Например, для провода из никелина диаметром 0,18 мм можно приблизительно считать, что площадь сечения равна 0,025 мм2, сопротивление одного метра 18 Ом, а допустимый ток равен 0,075 А.
2. Для другого значения плотности тока данные последнего столбца нужно соответственно изменить; например, при плотности тока, равной 6 А/мм2, их следует увеличить в два раза.
Пример 1. Найти сопротивление 30 м медного провода диаметром 0,1 мм.
Решение. Определяем по табл. 1 сопротивление 1 м медного провода, оно равно 2,2 Ом. Следовательно, сопротивление 30 м провода будет R = 30•2,2 = 66 Ом.
Расчет по формулам дает следующие результаты: площадь сечения провода: s= 0,78•0,12 = 0,0078 мм2. Так как удельное сопротивление меди равно 0,017 (Ом•мм2)/м, то получим R = 0,017•30/0,0078 = 65,50м.
Пример 2. Сколько никелинового провода диаметром 0,5 мм нужно для изготовления реостата, имеющего сопротивление 40 Ом?
Решение. По табл. 1 определяем сопротивление 1 м этого провода: R= 2,12 Ом: Поэтому, чтобы изготовить реостат сопротивлением 40 Ом, нужен провод, длина которого l= 40/2,12=18,9 м.
Проделаем тот же расчет по формулам. Находим площадь сечения провода s= 0,78•0,52 = 0,195 мм2. А длина провода будет l = 0,195•40/0,42 = 18,6 м.