Если бы ни магнитные потоки, то вряд ли современная электротехника могла бы существовать. Работа генераторов и электродвигателей, электромагнитов и трансформаторов, измерительных приборов и датчиков Холла, - основана на использовании магнитного поля и свойствах магнитного потока.
Для того чтобы сконцентрировать и усилить магнитный поток, прибегают к применению ферромагнитных материалов. Из ферромагнитных материалов изготавливают магнитопроводы — тела нужных форм и размеров, сердечники, чтобы направить магнитные потоки той или иной величины в требуемом направлении. Такие тела, внутри которых проходят замкнутые линии магнитной индукции, и называются магнитными цепями.
Известные свойства магнитного поля позволяют вычислять магнитные потоки в различных магнитных цепях. Но для практической работы гораздо удобнее прибегнуть к общим следствиям и закономерностям для магнитных цепей, вытекающим из законов магнитного поля, нежели пользоваться этими законами каждый раз напрямую. Применение частных правил для магнитных цепей удобнее для решения типовых практических задач.
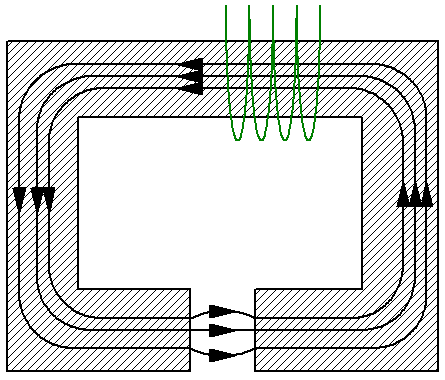
Для примера рассмотрим простую магнитную цепь, которая состоит из неразветвленного ярма сечением S, которое в свою очередь изготовлено из материала с магнитной проницаемостью мю. Ярмо имеет немагнитный зазор той же площади S, к примеру воздушный, причем магнитная проницаемость в зазоре — мю1 — отлична от магнитной проницаемости ярма. Здесь можно рассмотреть среднюю линию индукции и применить к ней теорему о магнитном напряжении:
Поскольку линии магнитной индукции всюду в цепи непрерывны, то величина магнитного потока как внутри ярма, так и в зазоре — одна и та же. Используем теперь формулы для магнитной индукции B и для магнитного потока Ф, чтобы выразить напряженность H магнитного поля через магнитный поток Ф.
Следующим шагом подставим полученные выражения в приведенную выше формулу теоремы о магнитном потоке:
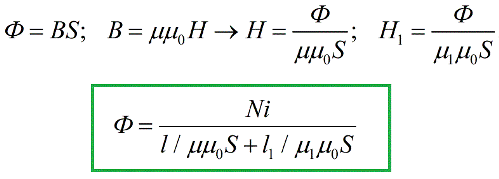
Мы получили формулу, которая очень похожа на известный в электротехнике закон Ома для участка замкнутой цепи, причем роль ЭДС играет здесь величина iN, называемая магнитодвижущей силой (или МДС) по аналогии с электродвижущей силой. В системе СИ магнитодвижущая сила измеряется в амперах.
Сумма, стоящая в знаменателе, есть ни что иное, как аналогия полного электрического сопротивления для электрической цепи, и для магнитной цепи она носит название, соответственно, полного магнитного сопротивления. Слагаемые в знаменателе — это магнитные сопротивления отдельных участков магнитной цепи.
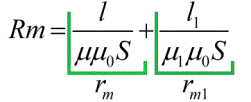
Магнитные сопротивления зависят от длины магнитопровода, от площади его сечения, и от магнитной проницаемости (аналогичной удельной электропроводности для обычного закона Ома). В итоге, можно записать формулу закона Ома, только для цепи магнитной:
То есть, формулировка закона Ома применительно к магнитной цепи звучит так: «в магнитной цепи без разветвлений магнитный поток равен частному от деления МДС на полное магнитное сопротивление цепи».
Из формул очевидно, что магнитное сопротивление в системe СИ измеряется в амперах на вебер, а полное магнитное сопротивление магнитной цепи численно равно сумме магнитных сопротивлений частей данной магнитной цепи.
Описанное положение справедливо для неразветвленной магнитной цепи, включающей в себя любое количество частей, при условии, что магнитный поток последовательно пронизывает все эти части. Если магнитопроводы соединены последовательно, то общее магнитное сопротивление находится путем сложения магнитных сопротивлений частей.
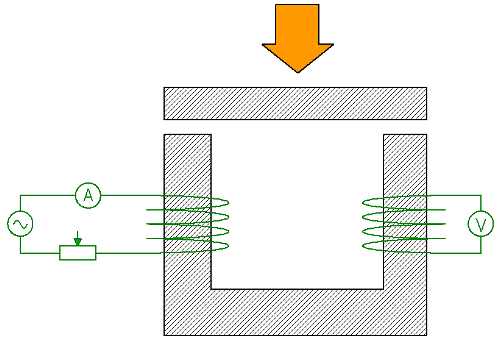
Рассмотрим теперь эксперимент, в котором демонстрируется влияние магнитного сопротивления частей цепи на полное магнитное сопротивление цепи. U-образный магнитопровод намагничивается обмоткой 1, питание (переменный ток) на которую подается через амперметр и реостат. Во вторичной обмотке 2 индуцируется ЭДС, и показания вольтметра, присоединенного к обмотке, как вы знаете, пропорциональны магнитному потоку в магнитопроводе.
Если теперь, сохранить ток в первичной обмотке неизменным, подстраивая его реостатом, и в то же время прижимать к магнитопроводу сверху железную пластину, то поскольку общее магнитное сопротивление цепи сильно уменьшится, показания вольтметра соответственно увеличатся.
Конечно, приведенные термины, такие как «магнитное сопротивление» и «магнитодвижущая сила», являются понятиями формальными, ибо ничего в магнитном потоке не движется, нет там движущихся частиц, это просто образное представление (вроде модели движения потока жидкости) для более ясного понимания закономерностей.
Физический же смысл приведенного эксперимента и других похожих экспериментов заключается в том, чтобы понять, как введение в магнитную цепь немагнитных зазоров и магнитных материалов влияет на магнитный поток в магнитной цепи.
Вводя например в магнитную цепь магнетик, мы добавляем к уже содержащимся в цепи телам дополнительные молекулярные токи, которые вносят дополнительные магнитные потоки. И формальные понятия, такие как «магнитное сопротивление» и «магнитодвижущая сила», оказываются очень удобными, когда требуется решить практическую задачу, поэтому они успешно и используются в электротехнике.
Андрей Повный