Из опыта известно, что возле постоянных магнитов, равно как и вблизи проводников с током, можно наблюдать физические эффекты, такие как механическое действие на другие магниты или проводники с током, а также появление ЭДС в движущихся в данном пространстве проводниках.
Необычное состояние пространства возле магнитов и проводников с током, называется магнитным полем, количественные характеристики которого легко определяются по данным явлениям: по силе механического воздействия или по электромагнитной индукции, по сути — по величине наводимой в движущемся проводнике ЭДС.
Явление наведения ЭДС в проводнике (явление электромагнитной индукции) проявляет себя в различных условиях. Вы можете двигать проводник через однородное магнитное поле, а можете просто изменять магнитное поле возле неподвижного проводника. В обоих случаях изменяющееся в пространстве магнитное поле станет наводить в проводнике ЭДС.
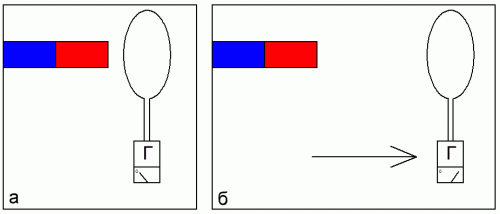
Простое экспериментальное приспособление для исследования данного явления изображено на рисунке. Здесь проводящее (медное) кольцо соединено своими выводами с баллистическим гальванометром, по отклонению стрелки которого можно будет судить о количестве электрического заряда, проходящего через эту нехитрую цепь. Сначала разместим кольцо центром в какой-нибудь точке пространства около магнита (положение а), затем резко отодвинем кольцо (в положение б). Гальванометр покажет значение прошедшего по цепи заряда Q.
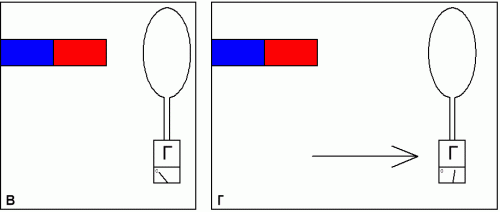
Теперь поместим кольцо в другую точку, чуть-чуть подальше от магнита (в положение в), и снова, с такой же скоростью, резко отодвинем его в сторону (в положение г). Отклонение стрелки гальванометра будут меньше чем в первом эксперименте. А если увеличить сопротивление петли R, например заменив медь на вольфрам, то перемещая кольцо аналогичным образом мы заметим, что гальванометр покажет заряд еще меньший, однако величина этого движущегося через гальванометр заряда в любом случае будет обратно пропорциональна сопротивлению петли.
Эксперимент отчетливо демонстрирует, что пространство вокруг магнита в каждой его точке обладает каким-то свойством, чем-то таким, что напрямую влияет на количество заряда, проходящего через гальванометр, когда мы отодвигаем кольцо от магнита. Назовем это что-то, находящееся около магнита, магнитным потоком, и обозначим его количественную величину буквой Ф. Отметим выявленную зависимость Ф~Q*R и Q~Ф/R.
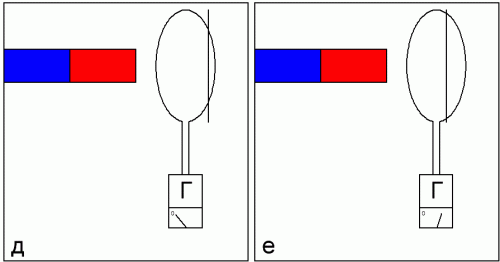
Усложним эксперимент. Закрепим медную петлю в определенной точке напротив магнита, рядом с ним (в положении д), но теперь будем изменять площадь петли (перекрывая ее часть проводником). Показания гальванометра будут пропорциональны изменению площади кольца (в положении е).
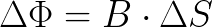
Следовательно действующий на петлю магнитный поток Ф от нашего магнита пропорционален площади петли. А вот магнитная индукция B, связанная с положением кольца относительно магнита, но не зависящая от параметров кольца, определяет свойство магнитного поля в каждой рассматриваемой точке пространства возле магнита.
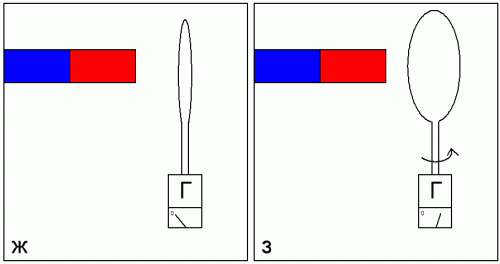
Продолжая эксперименты с медным кольцом, теперь будем изменять положение плоскости кольца относительно магнита в начальный момент (положение ж), и затем поворачивать его до положения вдоль оси магнита (положение з).
Заметим, что чем больше изменение угла между кольцом и магнитом — тем больше заряда Q протекает по цепи через гальванометр. Это значит, что магнитный поток через кольцо пропорционален косинусу угла между магнитом и нормалью к плоскости кольца.
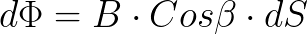
Таким образом можно заключить, что магнитная индукция B – есть величина векторная, направление которой в данной точке совпадает с направлением нормали к плоскости кольца в том его положении, когда при резком отодвигании кольца далеко от магнита, проходящий по цепи заряд Q максимален.
«
Подписывайтесь на наши каналы в Telegram:
Школа для электрика и Электрика, электромонтажные работы
Вместо магнита в эксперименте можно применять катушку электромагнита, отодвигать эту катушку или изменять в ней ток, усиливая или уменьшая таким образом магнитное поле, пронизывающее экспериментальный виток.
Площадь, пронизываемая магнитным полем, не обязательно может быть ограничена круглым витком, это может быть в принципе любая поверхность, магнитный поток через которую определяется тогда путем интегрирования:
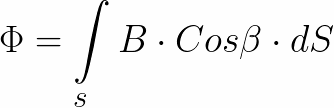
Выходит, что магнитный поток Ф — это поток вектора магнитной индукции B через поверхность S. А магнитная индукция B – это плотность магнитного потока Ф в данной точке поля. Магнитный поток Ф измеряется в единицах «Вебер» - Вб. Магнитная индукция B измеряется в единицах «Тесла» - Тл.
Если все пространство вокруг постоянного магнита или катушки с током исследовать подобным образом, при помощи витка с гальванометром, то можно построить в этом пространстве бесчисленное множество так называемых «магнитных линий» - линий вектора магнитной индукции B - направление касательных в каждой точке которых будет соответствовать направлению вектора магнитной индукции B в данных точках исследуемого пространства.
Разделив пространство магнитного поля воображаемыми трубками единичного поперечного сечения S=1, можно получить так называемые единичные магнитные трубки, оси которых называют единичными магнитными линиями. При помощи данного подхода можно наглядно изобразить количественную картину магнитного поля, и в этом случае магнитный поток будет равен количеству линий, проходящих через выбранную поверхность.
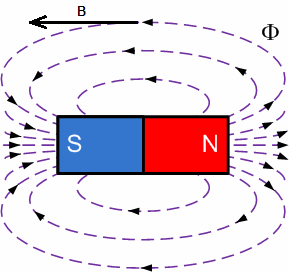
Магнитные линии непрерывны, они выходят из северного полюса и обязательно входят в южный, поэтому суммарный магнитный поток через любую замкнутую поверхность равен нулю. Математически это выглядит так:
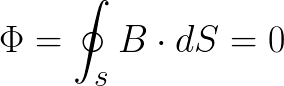
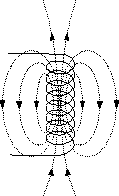
Рассмотрим магнитное поле, ограниченное поверхностью цилиндрической катушки. По сути — магнитный поток, пронизывающий поверхность, образованную витками данной катушки. В этом случае общую поверхность можно разделить на отдельные поверхности для каждого из витков катушки. На рисунке видно, что поверхности верхних и нижних витков катушки пронизываются четырьмя единичными магнитными линиями, а поверхности витков в середине катушки — восемью.
Чтобы найти величину полного магнитного потока через все витки катушки, необходимо суммировать магнитные потоки, пронизывающие поверхности каждого из ее витков, то есть магнитные потоки, сцепленные с отдельными витками катушки:
Ф = Ф1+Ф2+Ф3+Ф4+Ф5+Ф6+Ф7+Ф8, если в катушке 8 витков.
Для примера симметричной катушки, изображенной на предыдущем рисунке:
Ф верхних витков = 4+4+6+8 = 22;
Ф нижних витков = 4+4+6+8 = 22.
Ф общее = Ф верхних витков + Ф нижних витков = 44.
Здесь и вводится понятие «потокосцепление». Потокосцепление — это общий магнитный поток, сцепленный со всеми витками катушки, численно равный сумме магнитных потоков, сцепленных с отдельными ее витками:
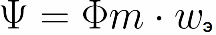
Фm - магнитный поток, создаваемый током через один виток катушки; wэ - эффективное число витков в катушке;
Потокосцепление — величина виртуальная, так как реально нет никакой суммы отдельных магнитных потоков, а есть общий магнитный поток. Тем не менее, когда реальное распределение магнитного потока по виткам катушки неизвестно, а известно потокосцепление, то катушку можно заменить эквивалентной, вычислив количество эквивалентных одинаковых витков, необходимых для получения требуемого общего магнитного потока.