В 1820 году, французские ученые Жан Батист Био и Феликс Савар, в ходе совместного проведения экспериментов по изучению магнитных полей постоянных токов, однозначно установили, что магнитную индукцию текущего по проводнику постоянного тока можно считать результатом общего действия всех участков данного проводника с током. Это значит, что магнитное поле подчиняется принципу суперпозиции (принципу наложения полей).

Магнитное поле, созданное группой проводников с постоянным током, имеет такую магнитную индукцию, что ее величина определяется как векторная сумма магнитных индукций, создаваемых каждым проводником индивидуально. То есть, индукцию В проводника с постоянным током можно справедливо представить векторной суммой элементарных индукций dB, принадлежащих элементарным участкам dl рассматриваемого проводника с постоянным током I.
Практически нереально выделить элементарный участок проводника с постоянным током, ведь постоянный ток всегда замкнут. Но можно измерить общую магнитную индукцию, создаваемую проводником, то есть порождаемую всеми элементарными кусочками данного проводника.
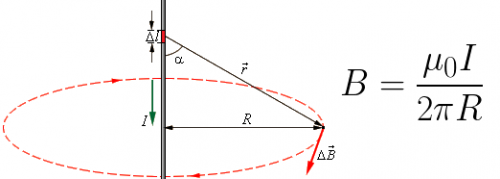
Таким образом, Закон Био-Совара позволяет найти величину магнитной индукции В от участка (известной длины dl) проводника, с заданным постоянным током I, на определенном расстоянии r от этого участка проводника и в определенном направлении наблюдения от выбранного участка (задается через синус угла между направлением тока и направлением от участка проводника к исследуемой точке пространства около проводника):
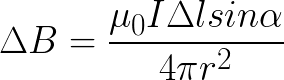
Экспериментально установлено, что направление вектора магнитной индукции с легкостью определяется правилом правого винта или буравчика: если направление поступательного движения буравчика при его вращении совпадает с направлением постоянного тока I в проводнике, то направление вращения рукоятки буравчика определяет направление вектора магнитной индукции B, получаемой от данного тока.
Магнитное поле прямолинейного проводника с током, а также иллюстрация применения закона Био-Савара к нему, представлены на рисунке:
Итак, если проинтегрировать, то есть сложить, вклады каждого из маленьких участков прямого проводника с постоянным током в общее магнитное поле, то получится формула для нахождения индукции магнитного поля проводника с током на определенном радиусе R от него.
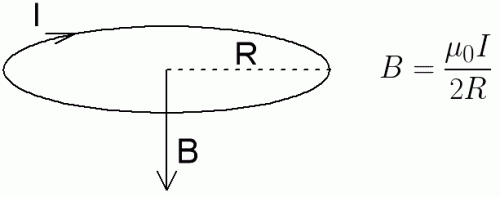
Таким же образом, при помощи закона Био-Савара, можно рассчитывать магнитные индукции от постоянных токов разнообразных конфигураций и в определенных точках пространства, например магнитная индукция в центре круглого витка с током находится по следующей формуле:
Направление вектора магнитной индукции легко находится по правилу буравчика, только теперь буравчик нужно вращать по направлению замкнутого тока, а поступательное движение буравчика покажет направление вектора магнитной индукции.
Часто расчеты касательно магнитного поля можно упростить, если принять во внимание симметрию конфигурации токов, данное поле порождающих. Здесь можно пользоваться теоремой о циркуляции вектора магнитной индукции (как теорема Гаусса в электростатике). Что такое «циркуляция вектора магнитной индукции»?
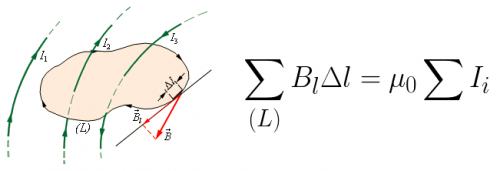
Выберем в пространстве некий замкнутый контур произвольной формы, и укажем условно положительное направление его обхода. Для каждой точки данного контура можно найти проекцию вектора магнитной индукции В на касательную к контуру в данной точке. Тогда сумма произведений данных величин на элементарные длины всех участков контура — это и будет циркуляция вектора магнитной индукции В по данному контуру:
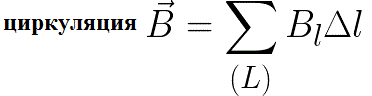
Практически, все токи, создающие здесь суммарное магнитное поле, могут либо пронизывать рассматриваемый контур, либо некоторые из них могут быть за его пределами. Согласно теореме о циркуляции: циркуляция вектора магнитной индукции В постоянных токов по замкнутому контуру численно равна произведению магнитной постоянной мю0 на сумму всех постоянных токов, данный контур пронизывающих. Эту теорему сформулировал Андре Мари Ампер в 1826 году:
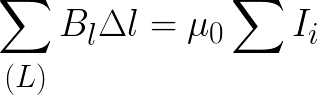
Рассмотрим приведенный выше рисунок. Здесь токи I1 и I2 пронизывают контур, но направлены они в разные стороны, значит имеют условно разные знаки. Положительный знак будет иметь тот ток, направление магнитной индукции у которого (по правилу буравчика) совпадает с направлением обхода выбранного контура. Для данной ситуации теорема о циркуляции примет вид:
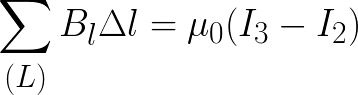
В общем виде теорема о циркуляции вектора магнитной индукции B следует из принципа суперпозиции магнитного поля и закона Био-Савара.
Для примера выведем формулу для магнитной индукции прямого проводника с постоянным током. Выберем контур в форме окружности, сквозь центр которой проходит данный проводник, причем проводник перпендикулярен плоскости контура.
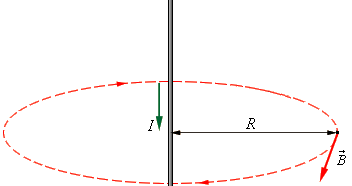
Таким образом, центр окружности лежит прямо по центру проводника, то есть в проводнике. Поскольку картина симметричная, то вектор В направлен по касательной к окружности, и его проекция на касательную, соответственно, везде одна и та же и равна длине самого вектора В. Теорема о циркуляции запишется так:
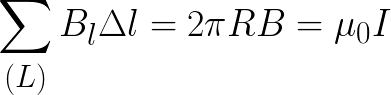
Отсюда и следует формула для магнитной индукции прямолинейного проводника с постоянным током (данная формула уже была приведена выше). Подобным образом с помощью теоремы о циркуляции можно легко находить магнитные индукции симметричных конфигураций постоянных токов, где картина силовых линий представляется легко.
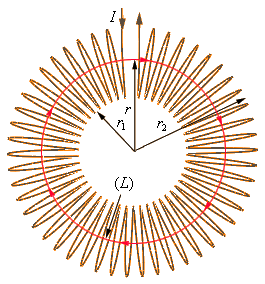
Одним из практически важных примеров применения теоремы о циркуляции является нахождение магнитного поля внутри тороидальной катушки индуктивности.
Допустим, имеется тороидальная катушка, намотанная виток к витку на картонный каркас в форме бублика, с числом витков N. Линии магнитной индукции при такой конфигурации замыкаются внутри бублика и по форме представляют собой концентрические (одна в другой) окружности.
Если смотреть вдоль по направлению вектора магнитной индукции на внутренней оси бублика, то окажется, что ток направлен везде по часовой стрелке (в соответствии с правилом буравчика). Рассмотрим одну из линий (показана красным цветом) магнитной индукции внутри катушки, и выберем ее в качестве круглого контура радиусом r. Тогда теорема о циркуляции для данного контура запишется так:
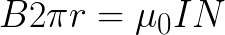
И магнитная индукция поля внутри катушки будет равна:
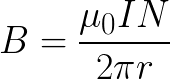
Для тонкой тороидальной катушки, где магнитное поле практически однородно по всему ее сечению, можно записать выражение магнитной индукции словно для бесконечно длинного соленоида с учетом числа витков на единицу длины — n:
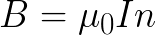
Рассмотрим теперь бесконечно длинный соленоид, где магнитное поле полностью находится внутри. Применим теорему о циркуляции к выбранному прямоугольному контуру.
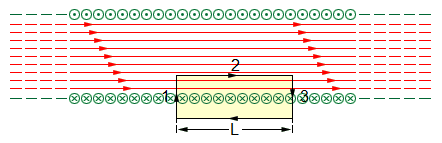
Здесь вектор магнитной индукции даст отличную от нуля проекцию только на сторону 2 (ее длина равна L). Использовав параметр n - «число витков на единицу длины», получим такой вид теоремы о циркуляции, который в итоге приводится к такому же виду, что и для очень тонкой тороидальной катушки:
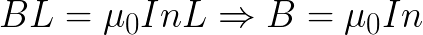




 Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное:
Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное: