Электрическая цепь — это совокупность устройств (элементов) и соединяющих их проводников, по которым может протекать электрический ток. Все элементы электрических цепей делят на пассивные и активные.
Активные элементы преобразуют различные виды энергии (механическую, химическую, световую и т.д.) в электрическую. На пассивных элементах электрическая энергия преобразуется в другие виды энергии. Активные элементы называют источниками, пассивные — потребителями или приемниками.
В теории цепей рассматриваются идеализированные модели электрических элементов. Это позволяет сделать описание элементов максимально простым. Более сложные, реальные элементы моделируются совокупностью идеализированных элементов.
Основными пассивными элементами электрических цепей являются резистор (резистивный элемент), катушка индуктивности (индуктивный элемент) и конденсатор (емкостный элемент). Элементы устанавливаются в электрическую цепь для формирования напряжения и тока заданной величины и формы (смотрите - Электрическая цепть и ее элементы).
Электрическая цепь состоит из ветвей и узлов. Ветвь — это участок электрической цепи (схемы), по которому течет один и тот же ток. Узел — соединение трех и более ветвей. На электрической схеме узел обозначается точкой (рис. 1).
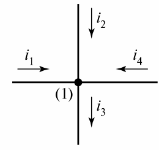
Рис. 1. Обозначение узла на схеме
При необходимости на схеме узлы нумеруются слева направо сверху вниз.
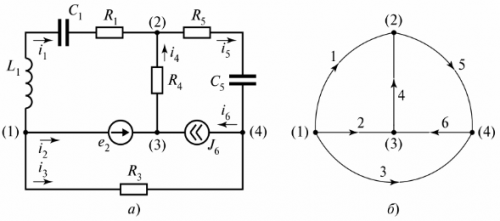
На рис. 2 изображена резистивно-емкостная ветвь, в которой протекает ток iС.
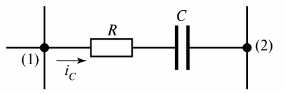
Рис. 2. Резистивно-емкостная ветвь
Можно дать еще одно определение ветви — это участок цепи между двумя смежными узлами (узлы (1) и (2) на рис. 2).
Контур — это любой замкнутый путь на электрической схеме. Контур может замыкаться через любые ветви, включая условные ветви, сопротивление которых равно бесконечности.
На рис. 3 изображена разветвленная электрическая цепь, которая состоит из трех ветвей.
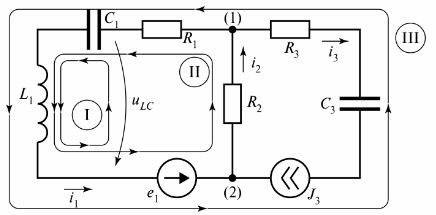
Рис. 3. Двухконтурная электрическая цепь
На схеме обозначены три контура, причем контур I замыкается через ветвь с бесконечным сопротивлением. Это ветвь обозначена как напряжение uLC.
Для схемы на рис. 3 можно составить множество контуров, замыкающихся через реальные или условные ветви, однако для расчета электрических испей используют понятие «независимый контур». Число независимых контуров схемы всегда определено как минимально необходимое для расчета.
Независимые контуры всегда замыкаются но ветвям, имеющим сопротивление, не равное бесконечности и каждый независимый контур включает в себя хотя бы одну ветвь, не входящую в другие контуры. Для сложных электрических цепей определить число независимых контуров можно, использую граф схемы.
Графом электрической цепи называется условное изображение схемы, в котором каждая ветвь заменяется отрезком линии. Элементы в ветвях не изображаются. Например, на рис. 4 изображены разветвленная электрическая цепь и ее граф.
Рис. 4. Разветвленная электрическая цепь: а - схема цепи, б - граф схемы
Для составления графа схемы нужно соединить узлы линиями ветвей без указания на них элементов. Ветви нумеруются, а направления токов на них указываются стрелками. Сам граф не имеет никакого физического смысла, однако с его помощью можно определить число и вид независимых контуров. Для этого составляется «дерево графа».
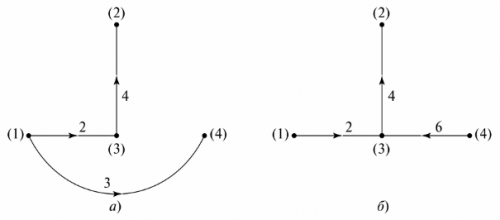
Дерево графа — это граф схемы, на котором узлы соединены ветвями таким образом, чтобы не получилось ни одного замкнутою контура. Вариантов изображения дерева графа может быть несколько. На рис. 5 изображены два возможных вариантадля схемы рис. 4.
Рис. 5. Дерево графа схемы
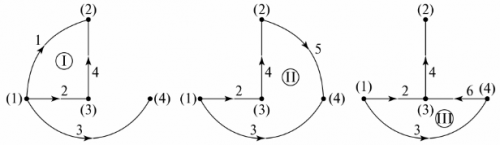
Число отсутствующих ветвей на дереве графа равно числу независимых контуров схемы. В примере — это три ветви, три независимых контура. Конфигурацию независимых контуров можно получить, последовательно соединяя узлы дерева графа ветвями, не обозначенными на дереве графа. Например, для дерева графа рис. 5, а независимые контуры изображены на рис. 6.
Рис. 6. Определение независимых контуров по дереву графа
Выбор варианта конфигурации независимых контуров для расчета цепи осуществляется при анализе схемы. Выбрать нужно такие контуры, чтобы расчет получился максимально простым, т.е. число зависимых уравнений в системе было минимальным.
Топологические уравнения устанавливают связь между напряжениями и токами цепи, причем число и вид уравнений не зависит от того, какие элементы входят в состав ветвей. К топологическим уравнениям относятся уравнения, составленные по законам Кирхгофа.