Законы Кирхгофа (правила Кирхгофа) устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа.
Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.
Наиболее частот законы Кирхгофа применяются для расчета разветвленных электрических цепей, так как вместе с законом Ома они позволяют определить величину и направление электрического тока в отдельных ветвях и величину электрического напряжения на зажимах отдельных элементов.
Анализ по законам Кирхгофа можно проводить как в цепях постоянного, так и переменного тока. В них напряжение и ток выражаются комплексными числами, которые представляют вектора, а полное сопротивление (импеданс) используется вместо электрического сопротивления.
Густав Роберт Кирхгоф (1824 – 1887)
Законы были названы в честь их первооткрывателя немецкого физика Густава Роберта Кирхгофа, впервые описавшего их в 1845 году.
Оба закона могут быть непосредственно выведены из уравнений Максвелла, сформулированных только в 1864 г. Кирхгоф создал законы как обобщение результатов, полученных Георгом Симоном Омом.
Вне электротехники законы Кирхгофа также используются в теории графов для анализа потоков. Можно даже сказать, что теория графов как таковая уходит своими корнями в законы Кирхгофа.
В дополнение к законам Кирхгофа для электрических цепей существует также закон Кирхгофа о тепловом излучении и другие эмпирические законы Кирхгофа, описывающие спектры излучения.
Для чего нужны законы Кирхгофа?
Разветвленные электрические цепи анализируются с использованием законов, определенных Густавом Кирхгофом. Законы Кирхгофа служат для определения величины и направления электрического тока в отдельных ветвях, определения величины электрического напряжения на зажимах отдельных элементов. Вместе с законом Ома законы Кирхгофа составляют основу теории электрических цепей.
Первый закон Кирхгофа
Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.
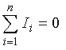
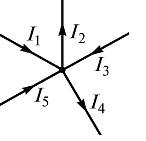
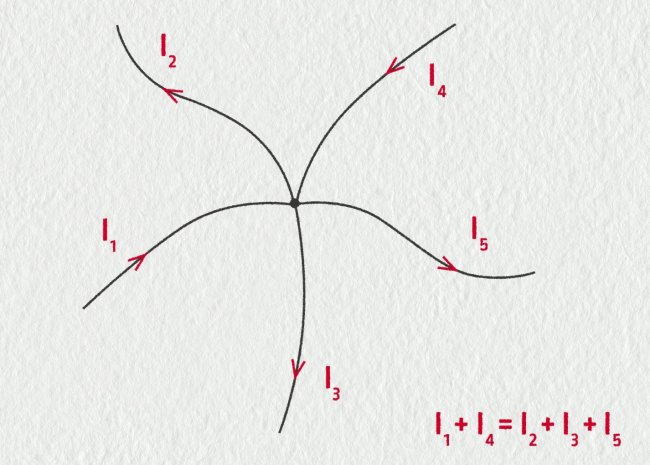
где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 - I2 + I3 - I4 + I5 = 0
Узел электрической цепи — это место, где встречаются не менее трех проводников. Проводящее соединение соседних узлов называется ветвью.
Рис. 1
В этом уравнении токи, направленные к узлу, приняты положительными.
Физически первый закон Кирхгофа – это закон непрерывности электрического тока. Он является выражением закона сохранения электрического заряда.
Сумма токов, втекающих в узел, равна сумме токов, выходящих из узла
Второй закон Кирхгофа
Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре
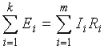
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
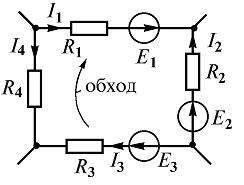
Рис. 2
Так, для замкнутого контура схемы (рис. 2) Е1 - Е2 + Е3 = I1R1 - I2R2 + I3R3 - I4R4
Замечание о знаках полученного уравнения:
1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.
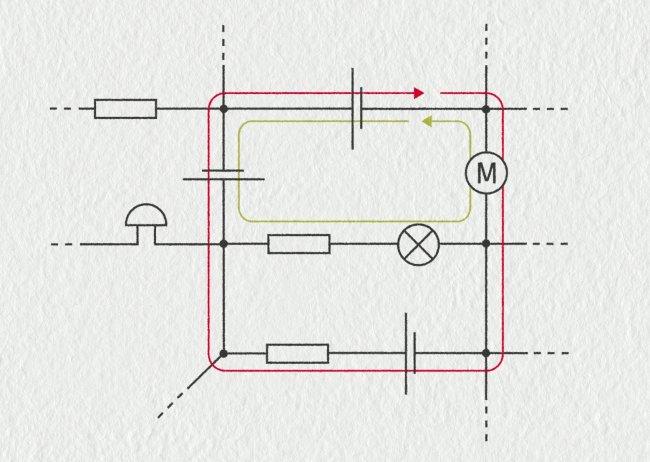
Простейшим примером замкнутого контура является простая последовательная цепь. Вообще говоря, замкнутый контур — это любой путь, ведущий к начальной точке через ответвления цепи. На рисунке вы видите часть сложной сети и в ней отмечены два разных контура.
Густав Кирхгоф
Молодой Густав Кирхгоф родился в относительно обеспеченной семье, что позволяло ему учиться в школе. Он получил образование в Кенигсбергском университете, нынешнем Калининграде. И поскольку ему повезло, его учителями были Карл Густав Якоб Якоби (брат Бориса Якоби) и Карл Фридрих Гаусс.
В возрасте двадцати двух лет молодой Кирхгоф сформулировал то, что сегодня мы называем законами, носящими его имя.
Он утверждал, что алгебраическая сумма токов в узле равна нулю. И что алгебраическая сумма напряжений в замкнутой части цепи равна нулю. Другими словами, то, что входит в узел, также выходит из него. И если в вашей схеме что-то пропадает, то наверняка нужно что-то туда добавить.
Хотя оба эти закона могут быть непосредственно выведены из так называемых уравнений Максвелла, сам великий Максвелл сформулировал их только двадцать лет спустя.
Кирхгоф также обнаружил, что если электрический сигнал проходит по проводу с абсолютно нулевым сопротивлением, он движется со скоростью света.
Но его интересовало и многое другое: например, он помог создать и использовать метод, который мы сейчас называем спектральным анализом. А когда ученые использовали его для наблюдения за звездами, Кирхгоф и Роберт Бунзен открыли химические элементы цезий и рубидий.
Однако он также посвятил себя оптике, так называемым проблемам черного тела, решал уравнения Максвелла для различных случаев, а в конце жизни стал уважаемым членом различных ученых обществ.
Расчет разветвленной электрической цепи с помощью законов Кирхгофа
Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.
Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b, следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.
Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только (y – 1) уравнений являются независимыми друг от друга.
Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b - (y - 1) = b - y +1.
Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.
Составим систему уравнений Кирхгофа для электрической цепи (рис. 3). Схема содержит четыре узла и шесть ветвей.
Поэтому по первому закону Кирхгофа составим y - 1 = 4 - 1 = 3 уравнения, а по второму b - y + 1 = 6 - 4 + 1 = 3, также три уравнения.
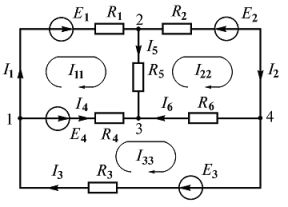
Произвольно выберем положительные направления токов во всех ветвях (рис. 4). Направление обхода контуров выбираем по часовой стрелке.
Рис. 3
Составляем необходимое число уравнений по первому и второму законам Кирхгофа
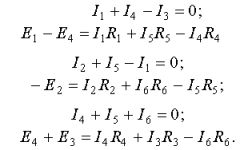
Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.
Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.
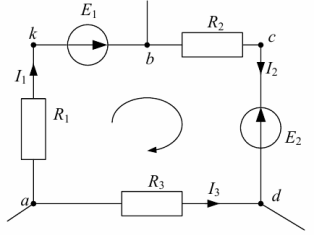
Рис. 4. Контур для построения потенциальной диаграммы
Потенциал любого узла принимаем равным нулю (например, а=0), выбираем обход контура и определяем потенциалы точек контура.
При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5).
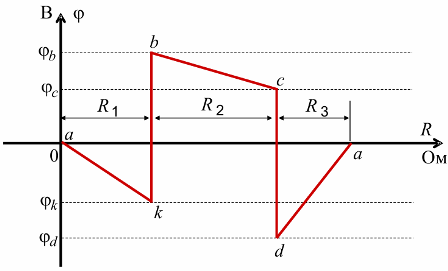
Рис. 5. Потенциальная диаграмма
Законы Кирхгофа в комплексной форме
Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.
Первый закон Кирхгофа: «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»
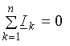
Второй закон Кирхгофа: «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».
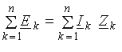





 Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное:
Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное: