Любой ток изменяющийся по величине является переменным. Но на практике под переменным током понимают такой ток, закон изменения которого во времени есть синусоидальная функция.
Математическое выражение для синусоидального тока можно записать в виде:
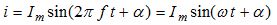
где, i - мгновенное значение тока, показывающее величину тока в конкретный момент времени, Im - амплитудное (максимальное) значение тока, выражение в скобках есть фаза, которая определяет значение тока в момент времени t, f - частота переменного тока, это величина, обратная периоду изменения синусоидальной величины Т, ω - угловая частота, ω = 2πf = 2π / T, α - начальная фаза, показывает значение фазы в момент времени t = 0.
Аналогичное выражение можно записать и для синусоидального переменного напряжения:
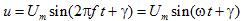
Мгновенные значения тока и напряжения условились обозначать строчными латинскими буквами i, u, а максимальные (амплитудные) значения – прописными печатными латинскими буквами I, U с индексом m.
Для измерения величины переменного тока чаще всего используют действующее (эффективное) значение, которое численно равно такому постоянному току, который за период переменного выделяет в нагрузке такое же количество тепла, что и переменный ток.
Действующее значение переменного тока:
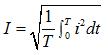
Для обозначения действующих значений тока и напряжения используют прописные печатные латинские буквы I, U без индекса.
В цепях синусоидального тока между амплитудным и действующим значениями существует взаимосвязь:
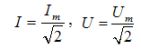
В цепях переменного тока изменение во времени питающего напряжения влечёт за собой изменение тока, а также магнитного и электрического полей, связанных с цепью. Результатом этих изменений является возникновение ЭДС самоиндукции и взаимоиндукции в цепях с катушками индуктивности, а в цепях с конденсаторами появляются зарядные и разрядные токи, которые создают сдвиг по фазе между напряжениями и токами в таких цепях.
Отмеченные физические процессы учитывают введением реактивных сопротивлений, в которых, в отличие от активных, не происходит превращение электрической энергии в другие виды энергии. Наличие тока в реактивном элементе объясняется периодическим обменом энергией между таким элементом и сетью. Все это усложняет расчёт цепей переменного тока, так как приходится определять не только величину тока, но и его угол сдвига по отношению к напряжению.
Все основные законы цепей постоянного тока справедливы и для цепей переменного тока, но только для мгновенных значений или значений в векторной (комплексной) форме. На основе этих законов можно составить уравнения, позволяющие осуществить расчёт цепи.
Как правило, целью расчёта цепи переменного тока является определение токов, напряжений, углов сдвига фаз и мощностей на отдельных участках. При составлении уравнений для расчёта таких цепей выбирают условные положительные направления ЭДС, напряжений и токов. Получаемые уравнения для мгновенных значений в установившемся режиме и синусоидальном входном напряжении будут содержать синусоидальные функции времени.
Аналитический расчёт тригонометрических уравнений неудобен, требует значительных затрат времени и поэтому не находит широкого распространения в электротехнике. Упростить анализ цепи переменного тока можно, используя тот факт, что синусоидальную функцию можно условно изобразить вектором, а вектор, в свою очередь, можно записать в виде комплексного числа.
Комплексным числом называют выражение вида:
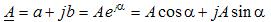
где a – вещественная (действительная) часть комплексного числа, j – мнимая единица, b – мнимая часть, A – модуль, α– аргумент, e – основание натурального логарифма.
Первое выражение представляет собой алгебраическую форму записи комплексного числа, второе – показательную, а третье – тригонометрическую. Для отличия, в комплексной форме записи подчеркивают букву, обозначающую электрический параметр.
Метод расчёта цепи, основанный на применении комплексных чисел, называется символическим методом. В символическом методе расчета все реальные параметры электрической цепи заменяют символами в комплексной форме записи. После замены реальных параметров цепи на их комплексные символы расчет цепей переменного тока выполняют методами, которые применяли для расчета цепей постоянного тока. Отличие состоит в том, что все математические операции необходимо выполнять с комплексными числами.
В результате расчета электрической цепи искомые токи и напряжения получаются в виде комплексных чисел. Реальные действующие значения тока или напряжения равны модулю соответствующего комплекса, а аргумент комплексного числа показывает угол поворота вектора на комплексной плоскости по отношению к положительному направлению вещественной оси. При положительном аргументе вектор поворачивается против часовой стрелки, а в случае отрицательного аргумента – по часовой.
Завершают расчёт цепи переменного тока, как правило, составлением баланса активных и реактивных мощностей, который позволяет проверить правильность вычислений.