Основные сведения из тригонометрии
Изучение переменного тока весьма затруднительно, если изучающий не усвоил основных сведений из тригонометрии. Поэтому основные положения тригонометрии, которые могут понадобиться в дальнейшем, мы приводим в начале этой статьи.
Известно, что в геометрии принято, рассматривая прямоугольный треугольник, называть сторону, лежащую против прямого угла, гипотенузой. Стороны, примыкающие к прямому углу, называются катетами. Прямой угол имеет 90°. Таким образом, на рис. 1 гипотенузой является сторона, обозначенная буквами Об, катетами же стороны аб и аО.
На рисунке отмечено, что прямой угол имеет 90°, два другие угла треугольника являются острыми и обозначены буквами α (альфа) и β (бета).
Если измерить в определенном масштабе стороны треугольника и взять отношение величины катета, лежащего против угла α, к величине гипотенузы, то такое отношение называют синусом угла α. Синус угла принято обозначать так: sin α. Следовательно, в прямоугольном треугольнике, который мы рассматриваем, синус угла равен:
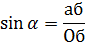
Если составить отношение, взяв величину катета аО, примыкающего к острому углу α, к гипотенузе, то это отношение называют косинусом угла α Косинус угла принято обозначать следующим образом: сos α. Таким образом, косинус угла а равен:
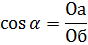
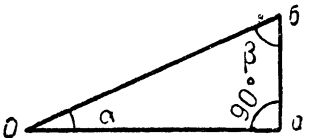
Рис. 1. Прямоугольный треугольник.
Зная синус и косинус угла α, можно определить величины катетов. Если умножить величину гипотенузы Об на sin α, то получим катет аб. Умножив гипотенузу на сos α, получим катет Оа.
Предположим, что угол альфа не остается постоянным, а постепенно изменяется, увеличиваясь. Когда угол равен нулю, синус его также равен нулю, так как нулю район противолежащий углу катет.
По мере того, как угол а будет возрастать, начнет увеличиваться и его синус. Наибольшее значение синуса получится, когда угол альфа станет прямым, то есть будет равен 90°. При этом синус равен единице. Таким образом, синус угла может иметь наименьшее значение—0 и наибольшее—1. Для всех промежуточных значений угла синус является правильной дробью.
Косинус угла будет наибольшим, когда угол равен нулю. При этом косинус равен единице, так как катет, прилежащий к углу, и гипотенуза в этом случае будут совпадать друг с другом, и отрезки, изображающие их, равны между собой. Когда угол равен 90°, косинус его равен нулю.
Графические способы изображения переменного тока
Синусоидальный переменный ток или э.д.с, изменяющиеся во времени, можно изобразить в виде синусоиды. Такой способ изображения часто применяется в электротехнике. Наряду с изображением переменного тока в виде синусоиды широко применяется также изображение такого тока в виде векторов.
Вектором называется величина, имеющая определенное значение и направление. Такую величину представляют в виде отрезка прямой линии со стрелкой на конце. Стрелка должна указывать направление вектора, а отрезок, измеренный в определенном масштабе, дает величину вектора.
Все фазы изменения переменного синусоидального тока за один период можно изобразить при помощи векторов, действуя следующим образом. Предположим, что начало вектора находится в центре окружности, а конец его лежит в самой окружности. Этот вектор, вращаясь по направлению против часовой стрелки, совершает полный оборот за время, соответствующее одному периоду изменения тока.
Проведем из точки, определяющей начало вектора, то есть из центра окружности О, две линии: одну горизонтальную, а другую вертикальную, как это изображено на рис 2.
Если для каждого положения вращающегося вектора из его конца, обозначенного буквою А, опускать перпендикуляры на вертикальную линию, то отрезки этой линии от точки О до основания перпендикуляра а будут давать нам мгновенные значения синусоидального переменного тока, а сам вектор OA в определенном масштабе изображает амплитуду этого тока, то есть его наибольшее значение. Отрезки Оа на вертикальной оси называются проекциями вектора OA на ось у.
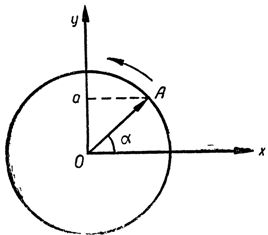
Рис. 2. Изображение изменений синусоидального тока с помощью вектора.
В справедливости изложенного выше не трудно убедиться, выполнив следующее построение. Рядом с окружностью на рисунке можно получить синусоиду, соответствующую изменению переменной э.д.с. за один период, если вдоль горизонтальной линии откладывать градусы, определяющие фазу изменения э.д.с, а в вертикальном направлении строить отрезки, равные величине проекции вектора OA на вертикальную ось. Выполнив такое построение для всех точек окружности, по которой скользит конец вектора OA, получим рис. 3.
Полный период изменения тока, а следовательно, и вращения изображающего его вектора, можно представить не только в градусах окружности, но и в радианах.
Углу в один градус соответствует 1/360 часть окружности, описанной из его вершины. Измерить тот или иной угол в градусах—это значит найти сколько раз такой элементарный угол содержится в измеряемом углу.
Однако, при измерении углов можно пользоваться не градусами, а радианами. При этом единицей, с которой сравнивают тот или иной угол, является угол, которому соответствует дуга, равная по длине радиусу любой окружности, описанной из вершины измеряемого угла.
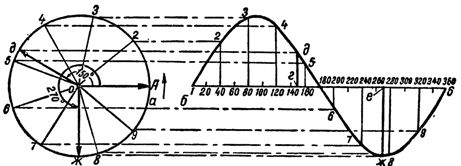
Рис. 3. Построение синусоиды э.д.с, изменяющейся по гармоническому закону.
Таким образом, полный угол, соответствующий любой окружности, измеренный в градусах, равен 360°. Этот же угол, измеренный в радианах, равен 2 π — 6,28 радиан.
О положении вектора в данный момент можно судить по угловой скорости его вращения и по времени, которое прошло от начала вращения, то есть с начала периода. Если обозначить угловую скорость вектора буквой ω (омега), а время с начала периода буквой t, то угол поворота вектора по отношению к его исходному положению можно определить как произведение:
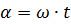
Угол поворота вектора определяет его фазу, которой соответствует то или иное мгновенное значение силы тока. Следовательно, угол поворота или фазовый угол позволяет судить о том, какое мгновенное значение имеет сила тока в интересующий нас момент времени. Фазовый угол часто называют просто фазой.
Выше было показано, что угол полного оборота вектора, выраженный в радианах, равен 2π. Этому полному обороту вектора соответствует один период изменения переменного тока. Умножив угловую скорость ω на время T соответствующее одному периоду, получим полный оборот вектора переменного тока, выраженный в радианах;
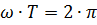
Отсюда не трудно определить, что угловая скорость ω равна:
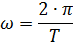
Заменив период Т отношением 1/f, получим:
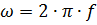
Угловая скорость ω в соответствии с этим математическим соотношением часто называется угловой частотой.
Векторные диаграммы
Если в цепи переменного тока действует не один какой-либо ток, а два или несколько, то их взаимное соотношение удобно представлять графически. Графическое изображение электротехнических величин (тока, э.д.с. и напряжения) можно осуществлять двумя способами. Один из этих способов — вычерчивание синусоид, показывающих все фазы изменения электротехнической величины в течение одного периода. На таком рисунке можно увидеть прежде всего какое соотношение максимальных значений исследуемых токов, э.д.с. и напряжений.
На рис. 4 изображены две синусоиды, характеризующие изменения двух разных переменных токов. Эти токи имеют одинаковый период и совпадают по фазе, но максимальные значения их разные.
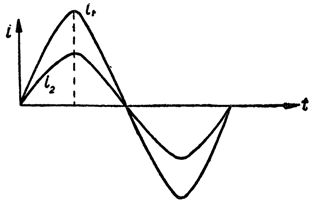
Рис. 4. Синусоиды токов, совпадающих по фазе.
Ток I1 имеет большую амплитуду, чем ток I2. Однако не всегда токи или напряжения могут совпадать по фазе. Сплошь и рядом бывает так, что фазы у них разные. В этом случае говорят, что они сдвинуты по фазе. На рис. 5 изображены синусоиды двух токов, сдвинутых по фазе.
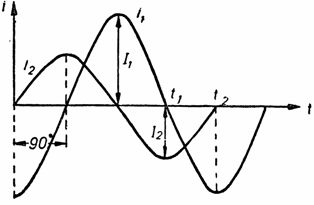
Рис. 5. Синусоиды токов, сдвинутых по фазе на 90°.
Угол сдвига фаз между ними равен 90°, что составляет одну четверть периода. На рисунке видно, что максимальное значение тока I2 наступает раньше на четверть периода, чем максимальное значение тока I1. Ток I2 опережает по фазе ток I1 на четверть периода, то есть на 90°. Это же соотношение между токами можно изобразить при помощи векторов.
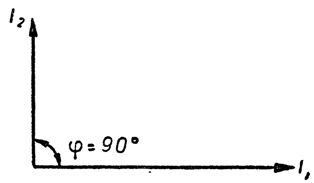
На рис. 6 изображены два вектора тех же токов. Если вспомнить, что направление вращения векторов условились принимать против часовой стрелки, то становится совершенно очевидным, что вектор тока I2, вращаясь в условном направлении идет впереди вектора тока I1. Ток I2 опережает ток I1. На этом же рисунке видно, что угол опережения равен 90°. Этот угол и является углом сдвига фаз между I1 и I2. Угол сдвига фаз обозначают буквой φ (фи). Такой способ изображения электротехнических величин при помощи векторов называют векторной диаграммой.
Рис. 6. Векторная диаграмма токов, сдвинутых по фазе на 90°.
При вычерчивании векторных диаграмм совершенно не обязательно изображать на рисунке окружности, по которым скользят концы векторов в процессе воображаемого нами их вращения.
Пользуясь векторными диаграммами, не следует забывать, что на одной диаграмме можно изображать только электрические величины, имеющие одинаковую частоту, т. е. одинаковую угловую скорость вращения векторов.