Применение векторных диаграмм при расчете и исследовании электрических цепей переменного тока позволяет наглядно представлять рассматриваемые процессы и упрощать производимые электротехнические расчеты.
При расчете цепей переменного тока часто приходится суммировать (или вычитать)
несколько однородных синусоидально изменяющихся величин одной и той же частоты,
но имеющих разные амплитуды и начальные фазы.
Такую задачу можно решать аналитическим путем тригонометрических
преобразований или геометрически.
Геометрический метод более прост и нагляден, чем аналитический.
Векторные диаграммы являются совокупностью векторов, изображающих действующие синусоидальные ЭДС и токи или их амплитудные значения.
Гармонически изменяющееся напряжение определяется выражением u = Um sin (ωt + ψи).
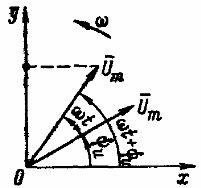
Расположим под углом ψи относительно положительной оси абсцисс х вектор Um, длина которого в произвольно выбранном масштабе равна амплитуде изображаемой гармонической величины (рис. 1). Положительные углы будем откладывать в направлении против вращения часовой стрелки, а отрицательные — по часовой стрелке. Предположим, что вектор Um, начиная с момента времени t = 0, вращается вокруг начала координат против часовой стрелки с постоянной частотой вращения ω, равной угловой частоте изображаемого напряжения. В момент времени t вектор Um повернется на угол ωt и будет расположен под углом ωt + ψи по отношению к оси абсцисс. Проекция этого вектора на ось ординат в выбранном масштабе равна мгновенному значению изображаемого напряжения: u = Um sin (ωt + ψи).
Рис. 1. Изображение синусоидального напряжения вращающегося вектора
Следовательно, величину, изменяющуюся гармонически во времени, можно изображать вращающимся вектором. При начальной фазе, равной нулю, когда u = 0, вектор Um для t = 0 должен быть расположен на оси абсцисс.
График зависимости любой переменной (в том числе и гармонической) величины от времени называется временной диаграммой. Для гармонических величин по оси абсцисс удобнее откладывать не само время t, а пропорциональную ему величину ωt . Временные диаграммы полностью определяют гармоническую функцию, так как дают представление о начальной фазе, амплитуде и о периоде.
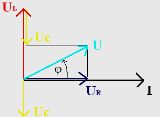
Обычно при расчете цепи нас интересуют только действующие ЭДС, напряжения и токи или амплитуды этих величин, а также их сдвиг по фазе относительно друг друга. Поэтому обычно рассматриваются неподвижные векторы для некоторого момента времени, который выбирается так, чтобы диаграмма была наглядной. Такая диаграмма называется векторной диаграммой. При этомуглы сдвига по фазе откладываются в направлении вращения векторов (против часовой стрелки), если они положительные, и в обратном направлении, если они отрицательные.
Если, например, начальный фазовый угол напряжения ψи больше начального фазового угла ψi то сдвиг по фазе φ = ψи - ψi и этот угол откладывается в положительном направлении от вектора тока.
При расчете цепи переменного тока часто приходится складывать ЭДС, токи или напряжения одной и той же частоты.
Предположим, что требуется сложить две ЭДС: e1 = E1m sin (ωt + ψ1e)и e2 = E2m sin (ωt + ψ2e).
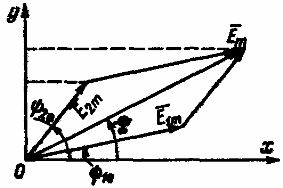
Такое сложение можно осуществить аналитически и графически. Последний способ более нагляден и прост. Две складываемые ЭДС е1 и е2 в определенном масштабе представлены векторами E1mE2m (рис. 2). При вращении этих векторов с одной и той же частотой вращения, равной угловой частоте, взаимное расположение вращающихся векторов остается неизменным.
Рис. 2. Графическое сложение двух синусоидальных ЭДС одинаковой частоты
Сумма проекций вращающихся векторов E1m и E2m на ось ординат равна проекции на ту же ось вектора Em, являющегося их геометрической суммой. Следовательно, при сложения двух синусоидальных ЭДС одной и той же частоты получается синусоидальная ЭДС той же частоты, амплитуда которой изображается вектором Em, равным геометрической сумме векторов E1m и E2m: Em = E1m + E2m.
Векторы переменных ЭДС и токов являются графическими изображениями ЭДС и токов в отличие от векторов физических величин, имеющих определенное физическое значение: вектора силы, напряженности поля и других.
Указанный способ можно применить для сложения и вычитания любого числа ЭДС и токов одной частоты. Вычитание двух синусоидальных величин можно представить в виде сложения: e1- e2 = e1+ (- e2), т. е. уменьшаемая величина складывается с вычитаемой, взятой с обратным знаком. Обычно векторные диаграммы строятся не для амплитудных значений переменных ЭДС и токов, а для действующих величин, пропорциональных амплитудным значениям, так как все расчеты цепей обычно выполняются для действующих ЭДС и токов.