Переменный ток можно выразить математически с помощью уравнения:
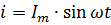
где ω — угловая частота, равная
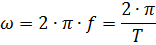
По этому уравнению можно найти мгновенное значение переменного тока в любой момент времени t. Величина ωt, стоящая под знаком синуса, определяет эти мгновенные значения тока и является фазовым углом (или фазой). Он выражается в радианах или градусах.
Для переменного синусоидального напряжения или для ЭДС можно написать такие же уравнения:
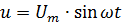
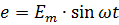
Во всех приведенных уравнениях вместо синуса можно поставить косинус. Тогда начальному моменту (при t = 0) будет соответствовать амплитудная фаза, а не нулевая.
Воспользуемся уравнением переменного тока для определения мощности этого тока и для доказательства соотношения между амплитудными и действующими значениями.
Мгновенная мощность переменного тока, т. е. его мощность в любой момент времени, равна
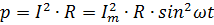
По формуле
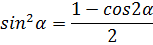
представим выражение для мощности в следующем виде:
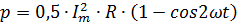
Полученная формула показывает, что мощность колеблется с двойной частотой. Это нетрудно понять. Ведь мощность при постоянном сопротивлении R определяется только величиной тока i и не зависит от направления тока. Сопротивление нагревается при любом направлении тока. Формула мощности отражает это тем, что i2 всегда является величиной положительной независимо от знака тока. Следовательно, за один период мощность дважды становится равной нулю (когда i = 0) и дважды достигает максимального значения (при i = Im и i = —Im), т. е. изменяется с удвоенной частотой по сравнению с частотой самого тока.
Найдем теперь среднее значение (т. е. среднее арифметическое) мощности переменного тока за один период. Среднее значение cos ωt за один период (или за целое число периодов) равно нулю, так как косинус принимает за один полупериод ряд положительных значений, а за другой полупериод — точно такие же отрицательные значения. Ясно, что среднее арифметическое всех этих значений равно нулю, а выражение Im2R/2 является величиной постоянной. Оно и представляет собой среднюю мощность переменного тока за один полупериод или за целое число полупериодов
Если представить, что Im2/2 есть квадрат действующего значения переменного тока I, т. е. написать I2 = Im2/2, то отсюда получим:
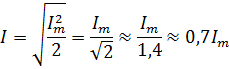
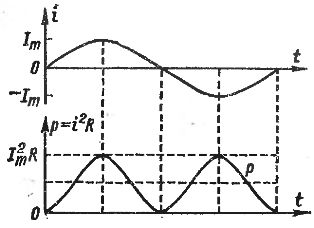
Приведенные выше соотношения можно проиллюстрировать. На рис. 1 даны графики переменного тока i и его мгновенной мощности р.
Рис. 1. Изменение мгновенной мощности переменного тока за один период
Графики мощности показывают, что величина р действительно колеблется с удвоенной частотой в пределах от 0 до Im2R, а среднее значение мощности, отмеченное жирной штриховой линией, равно Im2R/2