Коэффициентом мощности или косинусом фи, применительно к потребителю синусоидального переменного тока, называется отношение активной потребляемой мощности P к полной мощности S, которая поставляется к данному потребителю сетью.
Полную мощность S, в общем случае, можно определить как произведение действующих (среднеквадратических) значений тока I и напряжения U в рассматриваемой цепи, а активную мощность P — как безвозвратно расходуемую в потребителе на совершение работы.
Реактивная же мощность Q, хотя и является частью полной мощности, однако на совершение работы она не расходуется, а участвует лишь в создании переменных электрического и магнитного полей в некоторых элементах цепи потребителя.
Кроме непосредственного измерения коэффициента мощности при помощи электродинамических приборов — фазометров, есть вполне логичные косвенные методы, позволяющие математически точно узнать значение этой столь важной электротехнической величины, характеризующей потребитель в цепи синусоидального переменного тока.
Давайте же рассмотрим данные косвенные методы более подробно, разберемся в принципе измерения коэффициента мощности косвенным путем.
Метод вольтметра, амперметра и ваттметра
Электродинамический ваттметр с добавочным активным сопротивлением в цепи своей подвижной катушки показывает величину исключительно активной потребляемой в цепи переменного тока мощности P.
Если теперь с помощью вольтметра и амперметра измерить среднеквадратические значения тока I и напряжения U, действующих в цепи исследуемой нагрузки, то перемножив два данных параметра получим как раз полную мощность S.
Тогда коэффициент мощности (косинус фи) данной нагрузки может быть легко найден с использованием формулы:
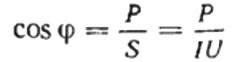
Тут же при желании можно найти и величину реактивной мощности Q, полное сопротивление цепи z по закону Ома, а также активное и реактивное сопротивление, просто построив или представив треугольник сопротивлений, а далее воспользовавшись теоремой Пифагора:
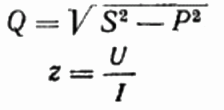
Метод счетчика и амперметра
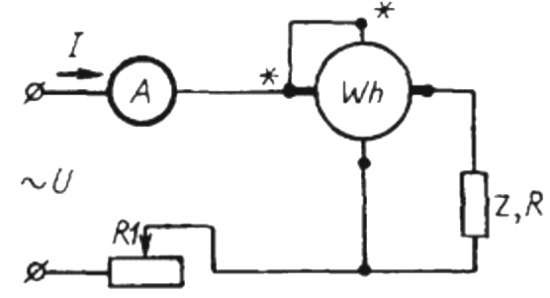
Чтобы воспользоваться данным методом, необходимо собрать схему, в которой последовательно с нагрузкой Z и амперметром подключить простейший счетчик электроэнергии Wh.
За некоторый промежуток времени t, порядка минуты, нужно будет подсчитать количество оборотов диска N, которое покажет количество потребленной за данное время активной энергии (то есть уже с учетом коэффициента мощности).
Здесь: количество оборотов диска N, коэффициент k – количество энергии за оборот, I и U - среднеквадратические ток и напряжение соответственно, t – время счета оборотов, косинус фи — коэффициент мощности:
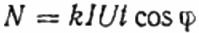
После этого, вместо исследуемого потребителя Z, через тот же счетчик в цепь включают активную нагрузку R, но не напрямую, а через реостат R1 (добиваясь такого же тока I, что и в первом случае, с потребителем Z). Поддерживают число оборотов диска N1 за аналогичное время t. Но здесь, поскольку нагрузка активная, косинус фи (коэффициент мощности) заведомо равен 1. Поэтому:
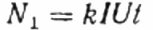
Далее записывают отношение оборотов диска счетчика за один и тот же промежуток времени в первом и во втором случае. Это и будет косинус фи, то есть коэффициент мощности первой нагрузки (относительно чисто активной нагрузки с тем же током):
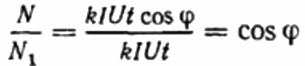
Метод трех амперметров
Для определения коэффициента мощности в цепи синусоидального тока при помощи трех амперметров, прежде всего необходимо собрать следующую цепь:
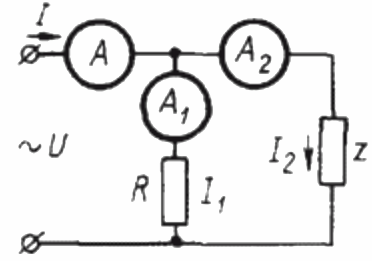
Здесь Z - потребитель, коэффициент мощности которого необходимо определить, а R – чисто активная нагрузка.
Поскольку нагрузка R чисто активная, то ток I1 в каждый момент времени находится в фазе с приложенным к данному потребителю переменным напряжением U. При этом ток I равен геометрической сумме токов I1 и I2. Теперь построим на основании этого положения векторную диаграмму токов:
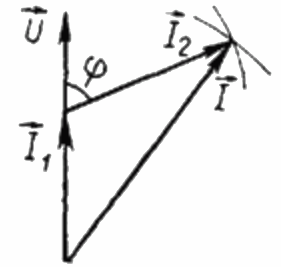
На векторной диаграмме токов, острый угол между током I1 и током I2 – есть угол фи, косинус которого (фактически - величину коэффициента мощности) можно найти из специальной таблицы значений тригонометрических функций, либо вычислить по формуле:
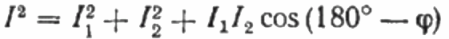
Отсюда можно выразить косинус фи, то есть искомый коэффициент мощности:
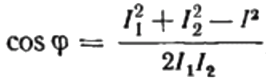
Знак найденного коэффициента мощности ( «+» или «-») укажет на характер нагрузки. Если коэффициент мощности (косинус фи) получился отрицательным — нагрузка имеет емкостной характер. Если коэффициент мощности — величина положительная — значит характер нагрузки индуктивный.