Тот, кто имеет представление о векторных диаграммах, легко заметит, что на них можно очень четко разглядеть прямоугольный треугольник напряжений, каждая из сторон которого отражает: полное напряжение цепи, напряжение на активном сопротивлении, и напряжение на реактивном сопротивлении.
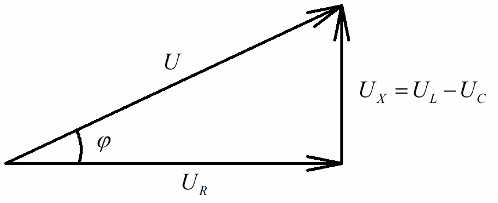
В соответствии с теоремой Пифагора, связь между этими напряжениями (между полным напряжением цепи и напряжением на ее участках) будет выглядеть так:
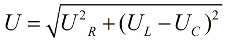
Если следующим шагом разделить значения этих напряжений на ток (ток через все участки последовательной цепи течет один и тот же), то по закону Ома получим значения сопротивлений, то есть теперь можно будет говорить о прямоугольном треугольнике сопротивлений:
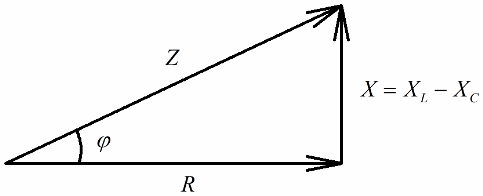
Аналогичным образом (как в случае с напряжениями) можно по теореме Пифагора установить связь между полным сопротивлением цепи и реактивными сопротивлениями. Связь выразится следующей формулой:
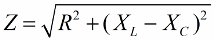
Далее умножим величины сопротивлений на ток, по сути — еще в определенное количество раз увеличим каждую из сторон прямоугольного треугольника. В итоге получим прямоугольный треугольник мощностей:
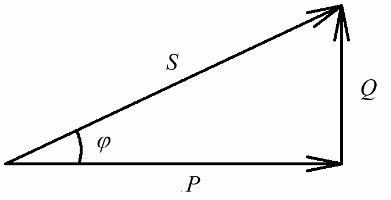
Активная мощность, выделяемая на активном сопротивлении цепи, связанная с необратимым преобразованием электрической энергии (в тепло, в совершение работы в установке) окажется явно связана с реактивной мощностью, участвующей в обратимом преобразовании энергии (создание магнитных и электрических полей в катушках и конденсаторах) и с полной мощностью, подводимой к электроустановке.
Активная мощность измеряется в ваттах (Вт), реактивная — в варах (ВАР — вольт-ампер реактивный), полная — в ВА (вольт-ампер).
По теореме Пифагора имеем право записать:
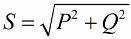
Теперь обратим внимание на то, что в треугольнике мощностей есть угол фи, косинус которого легко определить прежде всего через активную мощность и полную мощность. Косинус этого угла (косинус фи) называется коэффициентом мощности. Он показывает, какая доля полной мощности приходится на совершение полезной работы в электроустановке и в сеть не возвращается.
Очевидно, более высокий коэффициент мощности (максимум единица) свидетельствует о более высокой эффективности преобразования подводимой к установке энергии в работу. Если коэффициент мощности равен 1, то вся подводимая энергия идет на совершение работы.
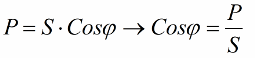
Полученные соотношения позволяют выразить ток потребления установки через коэффициент мощности, активную мощность и напряжение сети:
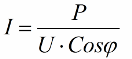
Так, чем меньше косинус фи, тем больший ток требуется от сети для совершения определенной работы. Практически этот фактор (максимальный ток от сети) ограничивает пропускную способность ЛЭП, и значит, чем меньше коэффициент мощности, тем выше загрузка линий и меньше полезная пропускная способность (низкий косинус фи порождает данное ограничение). Джоулевы потери в ЛЭП при снижении косинуса фи видны из следующей формулы:
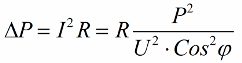
На активном R сопротивлении ЛЭП потери увеличиваются тем сильнее, чем выше ток I, хотя он для нагрузки и реактивный. Поэтому можно сказать, что при низком коэффициенте мощности попросту возрастает стоимость передачи электроэнергии. Значит повышение косинуса фи — это важная народно-хозяйственная задача.
Реактивную составляющую полной мощности желательно приблизить к нулю. Для этого электродвигатели и трансформаторы хорошо бы всегда использовать на полной загрузке и по окончании использования отключать, чтобы они не работали в холостую. На холостом ходу двигатели и трансформаторы имеют очень низкий коэффициент мощности. Один из путей повышения косинуса фи на потребителях — применение конденсаторных батарей и синхронных компенсаторов.
Андрей Повный


