Современный человек постоянно сталкивается в быту и на производстве с электричеством, пользуется приборами, потребляющими электрический ток и устройствами, вырабатывающими его. При работе с ними всегда надо учитывать их возможности, заложенные в технических характеристиках.
Одним из основных показателей любого электроприбора является такая физическая величина, как электрическая мощность. Ею принято называть интенсивность или скорость генерации, передачи либо преобразования электроэнергии в другие виды энергии, например, тепловую, световую, механическую.
Транспортировка или передача больших электрических мощностей в промышленных целях выполняется по высоковольтным линиям электропередач.
Преобразование электрической энергии осуществляется на трансформаторных подстанциях.
Потребление электричества происходит в бытовых и промышленных устройствах различного назначения. Одним из распространенных их видов являются лампы накаливания различных номиналов.
Электрическая мощность генераторов, линий электропередач и потребителей в цепях постоянного и переменного тока имеет один и тот же физический смысл, который в то же время выражается различными соотношениями, зависящими от формы составных сигналов. С целью определения общих закономерностей введены понятия мгновенных значений. Они еще раз подчеркивают зависимость скорости преобразований электроэнергии от времени.
Определение мгновенной электрической мощности
В теоретической электротехнике для вывода основных соотношений между током, напряжением и мощностью используются их представления в виде мгновенных величин, которые фиксируются в какой-то определенный временной момент.
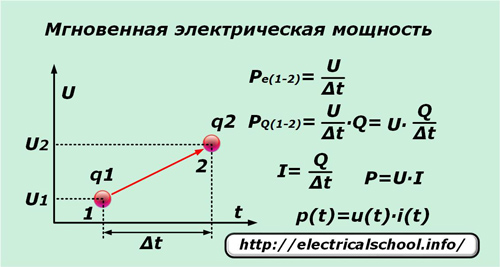
Если за очень короткий промежуток времени ∆t единичный элементарный заряд q под действием напряжения U перемещается из точки «1» в точку «2», то он совершает работу, равную разности потенциалов между этими точками. Разделив ее на промежуток времени ∆t, получим выражение мгновенной мощности для единичного заряда Pe(1-2).
Поскольку под действием приложенного напряжения перемещается не только единичный заряд, а все соседние, оказавшиеся под влиянием этой силы, количество которых удобно представить числом Q, то для них можно записать мгновенную величину мощности PQ(1-2).
Выполнив простые преобразования получим выражение мощности Р и зависимость ее мгновенного значения p(t) от составляющих произведения мгновенного тока i(t) и напряжения u(t).
Определение электрической мощности постоянного тока
В цепях постоянного тока величина падения напряжения на участке цепи и протекающего по нему тока не изменяется и остается стабильной, равной мгновенным значениям. Поэтому определить мощность в этой схеме можно перемножением этих величин или делением совершенной работы А на период времени ее выполнения, как показано на поясняющей картинке.
Определение электрической мощности переменного тока
Законы синусоидального изменения токов и напряжений, передаваемых по электрическим сетям, накладывают свое влияние на выражение мощности в таких цепях. Здесь действует полная мощность, которая описывается треугольником мощностей и состоит из активной и реактивной составляющих.
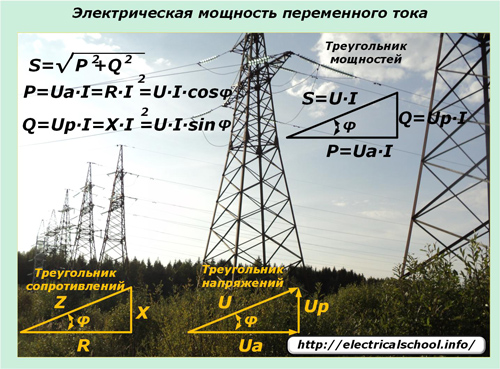
Электрический ток синусоидальный формы при прохождении по линиям электропередач со смешанными видами нагрузок на всех участках не изменяет форму своей гармоники. А падение напряжения на реактивных нагрузках сдвигается по фазе в определенную сторону. Понять влияние приложенных нагрузок на изменение мощности в цепи и ее направление помогают выражения мгновенных величин.
При этом сразу обратите внимание на то, что направление прохождения тока от генератора к потребителю и передаваемой мощности по созданной цепи — это совершенно разные вещи, которые в отдельных случаях могут не только не совпадать, но и направлены в противоположные стороны.
Рассмотрим эти взаимосвязи при их идеальном, чистом проявлении для разных видов нагрузок:
-
активной;
-
емкостной;
-
индуктивной.
Выделение мощности на активной нагрузке
Будем считать, что генератор вырабатывает идеальную синусоиду напряжения u, которая прикладывается к чисто активному сопротивлению цепи. Амперметр А и вольтметр V замеряют ток I и напряжение U в каждый момент времени t.
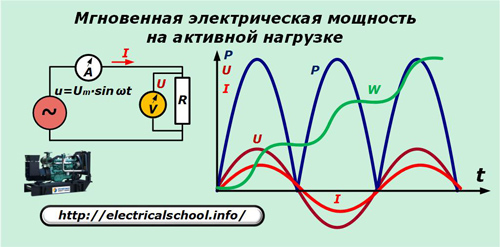
На графике видно, что синусоиды тока и падения напряжения на активном сопротивлении совпадают по частоте и фазе, совершая одинаковые колебания. Мощность же, выражаемая их произведением, колеблется с удвоенной частотой и всегда остается положительной.
p=u∙i=Um∙sinωt∙Um/R∙sinωt=Um2/R∙sin2ωt=Um2/2R∙(1-cos2ωt).
Если перейти к выражению действующего напряжения, то получим: p=P∙(1-cos2ωt).
Далее проинтегрируем мощность за период одного колебания Т и сможем заметить, что приращение энергии ∆W за этот промежуток увеличивается. С дальнейшим течением времени активное сопротивление продолжает потреблять новые порции электроэнергии, как показано на графике.
На реактивных нагрузках характеристики потребляемой мощности отличаются, имеют другой вид.
Выделение мощности на емкостной нагрузке
В схеме питания генератора заменим резистивный элемент конденсатором с емкостью С.
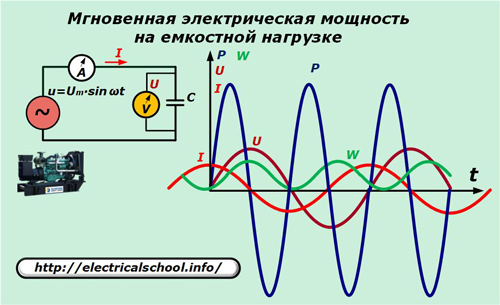
Соотношения между током и падением напряжения на емкости выражаются зависимостью: I=C∙dU/dt=ω∙C ∙Um∙cosωt.
Перемножим значения мгновенных выражений тока с напряжением и получим значение мощности, которая потребляется емкостной нагрузкой.
p=u∙i=Um∙sinωt∙ωC ∙Um∙cosωt=ω∙C ∙Um2∙sinωt∙cosωt=Um2/(2Xc)∙sin2ωt=U2/(2Xc)∙sin2ωt.
Здесь видно, что мощность совершает колебания относительно нуля с удвоенной частотой приложенного напряжения. Суммарное ее значение за период гармоники, как и приращение энергии, равно нулю.
Это означает, что энергия перемещается по замкнутому контуру цепи в обе стороны, но никакой работы не совершает. Подобный факт объясняется тем, что при нарастании напряжения источника по абсолютной величине мощность положительна, а поток энергии по цепи направляется в емкость, где происходит накопление энергии.
После того как напряжение переходит на падающий участок гармоники, из емкости начинается возврат энергии в контур к источнику. В обоих этих процессах полезная работа не совершается.
Выделение мощности на индуктивной нагрузке
Теперь в схеме питания заменим конденсатор индуктивностью L.
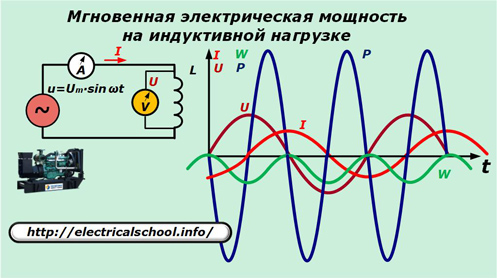
Здесь ток через индуктивность выражается соотношением:
I=1/L∫udt=-Um/ωL∙cos ωt.
Тогда получим
p=u∙i=Um∙sinωt∙ωC ∙(-Um/ωL∙cosωt)=-Um2/ωL∙sinωt∙cosωt=-Um2/(2XL)∙sin2ωt=-U2/(2XL)∙sin2ωt.
Полученные выражения позволяют увидеть характер изменения направления мощности и приращения энергии на индуктивности, которые совершают такие же бесполезные для выполнения работы колебания, как и на емкости.
Выделяемую на реактивных нагрузках мощность называют реактивной составляющей. Она в идеальных условиях, когда у соединительных проводов нет активного сопротивления, кажется безобидной и не создает никакого вреда. Но в условиях реального электроснабжения периодические прохождения и колебания реактивной мощности вызывают нагрев всех активных элементов, включая соединительные провода, на который затрачивается определенная энергия и снижается величина приложенной полной мощности источника.
Основное отличие реактивной составляющей мощности состоит в том, что она вообще не совершает полезной работы, а ведет к потерям электрической энергии и превышению нагрузок оборудования, особенно опасных в критических ситуациях.
По этим причинам для устранения влияния реактивной мощности используются специальные технические системы ее компенсации.
Выделение мощности на смешанной нагрузке
В качестве примера используем нагрузку на генератор с активно емкостной характеристикой.
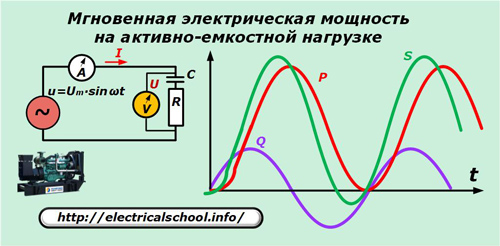
На приведенном графике не показаны для упрощения картины синусоиды токов и напряжений, но следует учесть, что при активно-емкостном характере нагрузки вектор тока опережает напряжение.
p=u∙i=Um∙sinωt∙ωC ∙Im∙sin(ωt+φ).
После преобразований получим: p=P∙(1- cos 2ωt)+Q ∙sin2ωt.
Эти два слагаемые в последнем выражении являются активной и реактивной составляющими мгновенной полной мощности. Только первая из них совершает полезную работу.
Приборы измерения мощности
Для анализа потребления электроэнергии и расчета за нее используются приборы учета, которые давно получили название «счетчики». Их работа основана на измерении действующих величин тока и напряжения и автоматическом перемножении их с выводом информации.
Счетчики отображают потребляемую мощность с учетом времени работы электроприборов по нарастающему принципу от момента включения электросчетчика под нагрузку.
Для замера в цепях переменного тока активной составляющей мощности используются ваттметры, а реактивной — варметры. Они имеют разные обозначения единиц измерения:
-
ватт (Вт, W);
-
вар (Вар, вар, var).
Чтобы определить полную мощность потребления, необходимо по формуле треугольника мощностей вычислить ее величину на основе показаний ваттметра и варметра. Она выражается в своих единицах — вольт-амперах.
Принятые обозначения единиц каждой помогают электрикам судить не только о ее величине, но и о характере составляющей мощности.