В проводниках — в металлах и электролитах, есть носители заряда. В электролитах это ионы, в металлах — электроны. Эти электрически заряженные частицы способны под действием внешнего электростатического поля перемещаться по всему объему проводника. Электроны проводимости в металлах, возникающие при конденсации паров металла, благодаря обобществлению валентных электронов, являются в металлах носителями заряда.

Напряженность и потенциал электрического поля в проводнике
В отсутствие внешнего электрического поля металлический проводник электрически нейтрален, поскольку внутри него электростатическое поле полностью компенсировано отрицательными и положительными зарядами внутри его объема.
Если внести металлический проводник во внешнее электростатическое поле, то электроны проводимости внутри проводника начнут перераспределяться, они придут в движение, и переместятся так, что всюду внутри объема проводника поле положительных ионов и поле электронов проводимости скомпенсирует в конце концов внешнее электростатическое поле.
Таким образом, внутри проводника, находящегося во внешнем электростатическом поле, в любой его точке, напряженность электрического поля E будет равна нулю. Разность потенциалов внутри проводника также будет равна нулю, то есть потенциал внутри станет постоянным. То есть видим, что диэлектрическая проницаемость металла стремится к бесконечности.
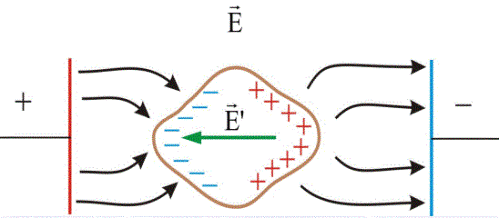
Но на поверхности проводника напряженность E будет направлена по нормали к этой поверхности, ибо в противном случае, составляющая напряженности, направленная по касательной к поверхности проводника привела бы к перемещению зарядов по проводнику, что противоречило бы реальному, статическому из распределению. Снаружи, вне проводника, электрическое поле есть, значит есть и вектор E, перпендикулярный поверхности.
В итоге, в установившемся состоянии, помещенный во внешнее электрическое поле металлический проводник будет иметь на своей поверхности заряд противоположного знака, а процесс этого установления длится наносекунды.
На том принципе, что внутрь проводника внешнее электрическое поле не проникает, основано электростатическое экранирование. Напряженность внешнего электрического поля Е компенсируется нормальным (перпендикулярным) электрическим полем на поверхности проводника En, а напряженность по касательной Eт равна нулю. Получается, что проводник в этой ситуации полностью эквипотенциален.
В любой точке такого проводника φ = const, поскольку dφ/dl = - E = 0. Поверхность проводника также эквипотенциальна, поскольку dφ/dl = - Eт = 0. Потенциал поверхности проводника равен потенциалу его объема. Нескомпенсированные заряды заряженного проводника, в такой ситуации, располагаются лишь на его поверхности, где носители заряда расталкиваются между собой кулоновскими силами.
« Подписывайтесь на наши каналы в Telegram: Школа для электрика и Электрика, электромонтажные работы
Согласно теореме Остроградского-Гаусса, суммарный заряд q внутри объема проводника равен нулю, поскольку E = 0.
Определение напряженности электрического поля вблизи проводника
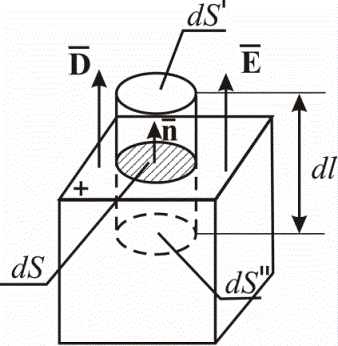
Если выделить на поверхности проводника площадку dS, и построить на ней цилиндр с перпендикулярными к поверхности образующими высотой dl, то будем иметь dS'=dS''=dS. Вектор напряженности электрического поля E перпендикулярен к поверхности, как и вектор электрического смещения D, пропорциональный E, следовательно поток D через боковую поверхность цилиндра будет нулевым.
Поток вектора электрического смещения Фd через dS'' тоже равен нулю, поскольку dS'' расположена внутри проводника, а там E = 0, значит и D = 0. Следовательно dФd сквозь замкнутую поверхность равен D через dS', dФd = Dn*dS. С другой стороны, по теореме Остроградского-Гаусса: dФd = dq = σdS, где σ — поверхностная плотность зарядов на dS. Из равенства правых частей уравнений следует, что Dn = σ, и тогда En = Dn/εε0 = σ/εε0.
Вывод: Напряженность электрического поля вблизи поверхности заряженного проводника прямопропорциональна поверхностной плотности зарядов.
Экспериментальная проверка распределения заряда на проводнике
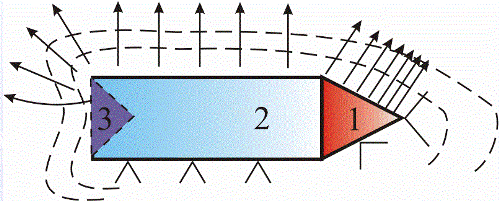
В местах с разной напряженностью электрического поля бумажные лепестки будут расходиться по-разному. На поверхности меньшего радиуса кривизны (1) — максимально, на боковой поверхности (2) — одинаково, здесь q = const, то есть заряд распределен равномерно.
Электрометр — прибор для измерения потенциала и заряда проводника, показал бы, что на острие заряд максимальный, на боковой поверхности — меньше, а заряд с внутренней поверхности (3) — нулевой. Напряженность электрического поля на острие заряженного проводника наибольшая.
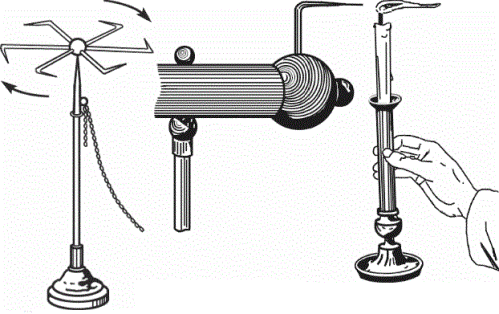
Поскольку на остриях напряженность электрического поля E велика, это приводит к утечке заряда и к ионизации воздуха, по этой причине, данное явление является зачастую нежелательным. Ионы уносят электрический заряд с проводника, возникает эффект ионного ветра. Наглядные демонстрации отражающие этот эффект: сдувание пламени свечи и колесо Франклина. Это хорошая основа для построения электростатического двигателя.
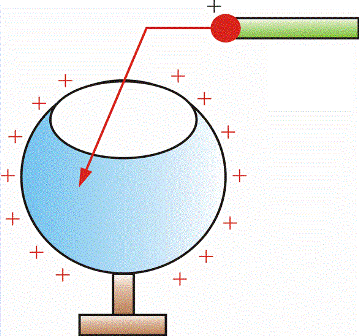
Если металлический заряженный шарик привести в соприкосновение с поверхностью другого проводника, то от шарика заряд частично передастся проводнику, и потенциалы этого проводника и шарика выровняются. Если же шарик привести в соприкосновение с внутренней поверхностью полого проводника, то весь заряд с шарика распределится полностью только по внешней поверхности полого проводника.
Так произойдет независимо от того, больше потенциал шарика чем у полого проводника или меньше. Даже если потенциал шарика до соприкосновения меньше, чем потенциал полого проводника, заряд с шарика перетечет полностью, поскольку при перемещении шарика в полость, экспериментатором будет совершена работа по преодолению сил отталкивания, то есть потенциал шарика будет расти, потенциальная энергия заряда возрастет.
В итоге, заряд перетечет от большего потенциала к меньшему. Если переносить теперь к полому проводнику следующую порцию заряда на шарике, то потребуется еще большая работа. В данном эксперименте наглядно отражается то, что потенциал является энергетической характеристикой.
Роберт Ван Де Грааф

Роберт Ван Де Грааф (1901 — 1967) — гениальный американский физик. В 1922 году Роберт окончил университет Алабамы, позже, с 1929 по 1931 год, работал в Принстонском университете, а с 1931 по 1960 — в Массачусетском технологическом институте. Ему принадлежит ряд научных исследований по ядерной и ускорительной технике, идея и реализация тандемного ускорителя ионов, а также изобретение высоковольтного электростатического генератора, генератора Ван Де Граафа.
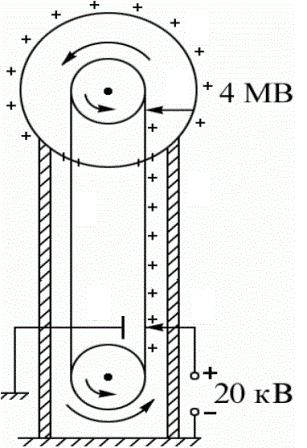
Принцип работы генератора Ван Де Граафа несколько напоминает эксперимент с перенесением заряда шариком в полую сферу, как в описанном выше эксперименте, но здесь процесс автоматизирован.
Лента транспортера заряжается положительно при помощи высоковольтного источника постоянного напряжения, затем заряд с движением ленты переносится внутрь большой металлической сферы, где острием же передается ей, и распределяется по внешней сферической поверхности. Так получают потенциалы относительно земли в миллионы вольт.
В настоящее время существуют ускорительные генераторы Ван Де Граафа, например в НИИ ядерной физики в Томске есть ЭСГ такого типа на миллион вольт, который установлен в отдельной башне.
« Подписывайтесь на наши каналы в Telegram: Школа для электрика и Электрика, электромонтажные работы
Электрическая емкость и конденсаторы
Как упоминалось выше, при сообщении проводнику заряда, на его поверхности появится некоторый потенциал φ. И у разных проводников этот самый потенциал будет различаться, даже если количество сообщаемого проводникам заряда будет одинаковым. В зависимости от формы и размеров проводника, потенциал может быть разным, однако так или иначе, он будет пропорционален заряду, а заряд будет пропорционален потенциалу.
Коэффициент пропорциональности называется электрической емкостью, электроемкостью, или просто емкостью (когда это со всей очевидностью подразумевается контекстом).
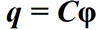
Электроемкостью называется физическая величина, равная численно заряду, который нужно сообщить проводнику, чтобы изменить его потенциал на единицу. В системе СИ электроемкость измеряется в фарадах (сейчас «фарад», раньше было «фарада»), и 1Ф = 1Кл/1В. Так, потенциал поверхности сферического проводника (шара) равен φш = q/4πεε0R, значит Сш = 4πεε0R.
Если принять R равным радиусу Земли, то электроемкость Земли, как уединенного проводника получится равной 700 мкф. Важно! Это электроемкость Земли, как уединенного проводника!
Если к одному проводнику поднести другой проводник, то из-за явления электростатической индукции электроемкость проводника возрастет. Так, два проводника, расположенные близко друг к другу, и представляющие собой обкладки, называются конденсатором.
Когда электростатическое поле сосредоточено между обкладками конденсатора, то есть внутри него, внешние тела не оказывают влияния на его электроемкость.
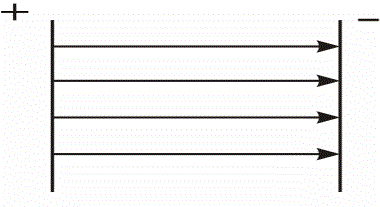
Конденсаторы бывают плоскими, цилиндрическими и сферическими. Поскольку электрическое поле сосредоточено внутри, между обкладками конденсатора, линии электрического смещения начинаясь на положительно заряженной обкладке конденсатора, заканчиваются на отрицательно заряженной его обкладке. Следовательно, заряды обкладок противоположны по знаку, но по величине одинаковы. И емкость конденсатора С = q/(φ1-φ2) = q/U.
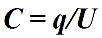
Формула емкости плоского конденсатора (для примера)
Поскольку напряженность электрического поля E между обкладками равна E = σ/εε0 = q/εε0S, а U = Ed, тогда C = q/U = q/(qd/εε0S) = εε0S/d.
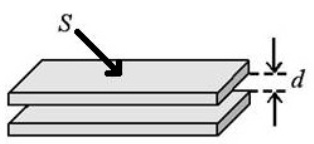
S – площадь обкладок; q – заряд конденсатора; σ — плотность заряда; ε – диэлектрическая проницаемость диэлектрика между обкладками; ε0 – диэлектрическая проницаемость вакуума.
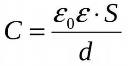
Энергия заряженного конденсатора
Замыкая обкладки заряженного конденсатора между собой проволочным проводником, можно наблюдать ток, который может быть такой силы, что мгновенно расплавит проволоку. Очевидно, конденсатор запасает энергию. Какова эта энергия количественно?
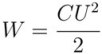
Если конденсатор заряжен, и затем разряжается, то U' – мгновенное значение напряжения на его обкладках. При прохождении между обкладками заряда dq, будет совершена работа dA = U'dq. Работа эта численно равна убыли потенциальной энергии, значит dA = - dWc. А поскольку q = CU, то dA = CU'dU', и полная работа А = ∫ dA. Проинтегрировав данное выражение, предварительно сделав подстановку, получим Wc = CU2/2.


