Подобно тому, как обладающее массой тело в механике сопротивляется ускорению в пространстве, проявляя инерцию, так же и индуктивность препятствует изменению тока в проводнике, проявляя ЭДС самоиндукции. Именно ЭДС самоиндукции противится как уменьшению тока, стремясь поддержать его, так и возрастанию тока, стремясь его уменьшить.
Дело в том, что в процессе изменения (увеличения или уменьшения) тока в контуре, изменяется и создаваемый этим током магнитный поток, локализованный главным образом в ограниченной данным контуром области. А раз магнитный поток возрастает или уменьшается, то он и наводит ЭДС самоиндукции (по правилу Ленца — против причины его вызывающей, то есть против упомянутого вначале тока) все в этом же контуре. А индуктивностью L здесь называют коэффициент пропорциональности между током I и полным магнитным потоком Ф, этим током порождаемым:
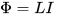
Итак, чем выше индуктивность контура — тем сильнее он, возникающим магнитным полем, препятствует изменению тока (это самое поле и создающему), и значит на изменение тока через бОльшую индуктивность, при одном и том же приложенном напряжении, потребуется больше времени. Верно и такое утверждение: чем выше индуктивность - тем большее напряжение возникнет на концах контура при изменении магнитного потока сквозь него.
Допустим, мы изменяем магнитный поток в определенной области с постоянной скоростью, тогда охватывая эту область разными контурами, большее напряжение получим на том контуре, индуктивность которого больше (на этом принципе работает трансформатор, катушка Румкорфа и т.д.).
Но как же рассчитать индуктивность контура? Как найти коэффициент пропорциональности между током и магнитным потоком? Первым делом вспомним, что индуктивность изменяется в Генри (Гн). На выводах контура индуктивностью 1 генри, если ток в нем изменить на один ампер за секунду, возникнет напряжение 1 вольт.
Величина индуктивности зависит от двух параметров: от геометрических размеров контура (длина, ширина, количество витков и т. д.) и от магнитных свойств среды (если например внутри катушки есть ферритовый сердечник — индуктивность ее будет больше, нежели если сердечника внутри нет).
Для расчета изготавливаемой индуктивности необходимо знать, какой формы будет сама катушка, и какой магнитной проницаемостю будет обладать среда внутри нее (относительная магнитная проницаемость среды — это коэффициент пропорциональности между магнитной проницаемостью вакуума и магнитной проницаемостью данной среды. Для разных материалов она, конечно, разная).
Давайте рассмотрим формулы для расчета индуктивностей наиболее распространенных форм катушек (цилиндрический соленоид, тороид и длинный проводник).
Вот формула для расчета индуктивности соленоида — катушки, у которой длина значительно превосходит диаметр:
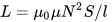
Как видно, зная количество витков N, длину намотки l и площадь сечения катушки S, найдем приблизительную индуктивность катушки без сердечника или с сердечником, при этом магнитная проницаемость вакуума есть величина постоянная:
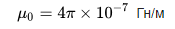
Индуктивность тороидальной катушки, где h – высота тороида, r – внутренний диаметр тороида, R – наружный диаметр тороида:
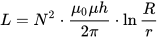
Индуктивность тонкого проводника (радиус сечения сильно меньше длины), где l - длина проводника, а r – радиус его сечения. Мю с индексами i и e – относительные магнитные проницаемости внутренней (internal, материал проводника) и внешней (external, материал снаружи проводника) сред:
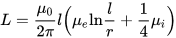
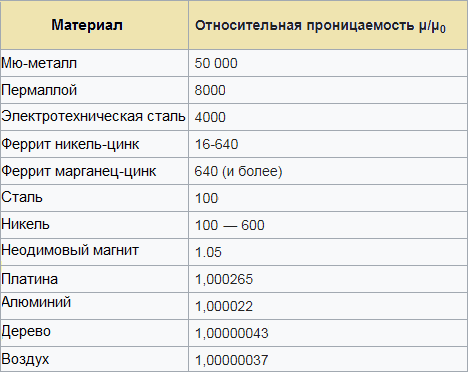
Таблица относительных магнитных проницаемостей поможет вам прикинуть, какой индуктивности можно ожидать от контура (проводника, катушки), применив тот или иной магнитный материал в качестве сердечника:
