Скалярные и векторные физические величины
Одной из основных целей физики является установление закономерностей наблюдаемых явлений. Для этого при рассмотрении различных случаев вводятся характеристики, определяющие течение физических явлений, а также свойства и состояние веществ и сред. Из этих характеристик можно выделить собственно физические величины и параметрические величины. Последние определяются так называемыми параметрами или постоянными.
Под собственно величинами подразумевают те характеристики явлений, которые определяют явления и процессы и могут существовать независимо от состояния среды и условий.
К таким, например, относятся электрический заряд, напряженность поля, индукция, электрический ток и т. д. Среда и условия, в которых протекают явления, определяемые данными величинами, могут изменить эти величины в основном только количественно.
Под параметрами будем подразумевать такие характеристики явлений, которые определяют свойства сред и веществ и влияют на соотношение между собственно величинами. Они не могут существовать самостоятельно и проявляются лишь в их действии на собственно величины.
К параметрам относятся, например, электрическая и магнитная постоянные, удельное электрическое сопротивление, коэрцитивная сила, остаточная индукция, параметры электрических цепей (сопротивление, проводимость, емкость, индуктивность на единицу длины или объема в данном устройстве) и др.
Значения параметров обычно зависят от условий, в которых протекает данное явление (от температуры, давления, влажности и т. п.), но при постоянстве этих условий параметры сохраняют свои значения неизменными и поэтому называются также постоянными.
Количественные (числовые) выражения величин или параметров называются их значениями.
Физические величины могут определяться двояко: одни — только числовым значением, а другие — как числовым значением, так и направлением (положением) в пространстве.
К первым относятся такие величины как масса, температура, сила электрического тока, электрический заряд, работа и т. д. Эти величины называются скалярными (или скалярами). Скалярная величина может быть выражена только в виде одного именованного числового значения.
Ко вторым величинам, называемым векторными, относятся сила, скорость, ускорение и т. д. Длина вектора в определенном масштабе равна числовому значению физической величины, которую данный вектор представляет, а стрелка показывает направление действия ее в пространстве.
Пример (сила Лоренца из статьи Напряженность электромагнитного поля):
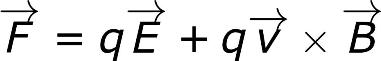
Скалярные величины и абсолютные значения векторных величин обычно обозначаются прописными буквами латинского алфавита, векторные же величины пишутся с черточкой или стрелкой над символом величины.
Скалярные и векторные поля
Поля в зависимости от вида физического явления, характеризующего поле, бывают скалярные или векторные.
В математическом представлении поле — это пространство, каждую точку которого можно охарактеризовать числовыми значениями.
Такое понятие поля может быть применено и при рассмотрении физических явлений. Тогда любое поле можно представлять как пространство, в каждой точке которого обнаруживается обусловленное данным явлением (источником поля) воздействие на некоторую физическую величину. Полю в таком случае присваивают название этой величины.
Так, нагретое тело, излучающее тепло, окружено полем, точки которого характеризуются температурой, поэтому такое поле называется температурным полем. Поле, окружающее тело, заряженное электричеством, в котором обнаруживается силовое воздействие на неподвижные электрические заряды, называется электрическим полем и т. п.
В соответствии с этим температурное поле вокруг нагретого тела, поскольку температура может быть представлена только как скаляр, является скалярным полем, а электрическое поле, характеризующееся действующими на заряды силами, имеющими определенное направление в пространстве, называется векторным.
«
Подписывайтесь на наши каналы в Telegram:
Школа для электрика и Электрика, электромонтажные работы
Примеры скалярных и векторных полей
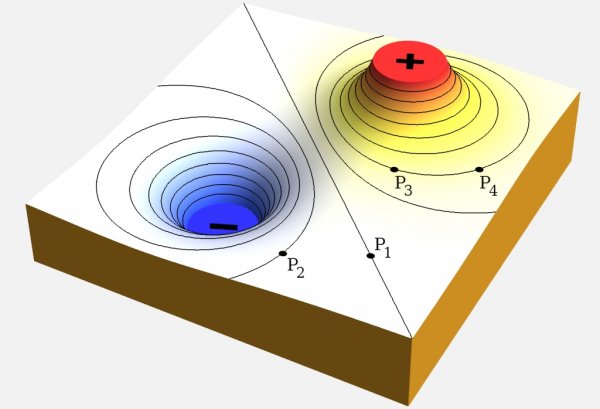
В качестве характерного примера скалярного поля можно привести температурное поле вокруг нагретого тела. Чтобы оценить количественно такое поле, у отдельных точек картины этого поля можно поставить цифры, равные температуре в этих точках.
Однако такой способ представления поля неудобен. Поэтому обычно поступают так: предполагают, что точки пространства, в которых температура одинакова, принадлежат одной поверхности. Подобные поверхности в данном случае можно назвать равнотемпературными. Линии, получающиеся при пересечении такой поверхности другой поверхностью, называются равнотемпературными линиями, или изотермами.
Обычно, если пользуются такими графиками, изотермы проводят через равные интервалы температуры (например, через каждые 100 град). Тогда густота линий у данной точки дает наглядное представление о характере поля (скорости изменения температуры).
Пример скалярного поля (результаты расчета освещенности в программе Dialux):
В качестве примеров скалярного поля можно еще привести гравитационное поле (поле силы притяжения Земли), а также электростатическое поле вокруг тела, которому сообщен электрический заряд, если каждую точку этих полей характеризовать скалярной величиной, называющейся потенциалом.
Для образования любого поля приходится затрачивать некоторое количество энергии. Эта энергия не исчезает, а накапливается в поле, распределяясь во всем его объеме. Она является потенциальной и может быть возвращена полем в виде работы сил поля при перемещении в нем масс или заряженных тел. Поэтому поле может быть оценено также потенциальной характеристикой, определяющей возможность поля совершать работу.
Поскольку обычно энергия в объеме поля распределена неравномерно, эту характеристику относят к отдельным точкам поля. Величину, представляющую собой потенциальную характеристику точек поля, называют потенциалом, или потенциальной функцией.
В применении к электростатическому полю наибольшее распространение получил термин "потенциал", а к магнитному полю — "потенциальная функция". Иногда последняя называется также энергетической функцией.
Потенциал отличается такой особенностью: значение его в поле непрерывно, без скачков, изменяется от точки к точке.
Потенциал точки поля определяют величиной работы, которую совершают силы поля при перемещении единичной массы или единичного заряда из данной точки в точку, где данное поле отсутствует (данная характеристика поля равна нулю), или которую нужно затратить, действуя против сил поля, чтобы перенести единичную массу или заряд в данную точку поля из точки, где действие данного поля равно нулю.
Работа — скалярная величина, поэтому и потенциал является скаляром.
Поля, точки которых могут быть охарактеризованы значениями потенциала, называются потенциальными полями. Поскольку все потенциальные поля являются скалярными, то термины "потенциальный" и "скалярный" синонимичны.
Как и в случае рассмотренного выше температурного поля, в любом потенциальном поле можно найти много точек с одинаковыми потенциалами. Поверхности, на которых располагаются точки равного потенциала, называются эквипотенциальными, а пересечение их с плоскостью чертежа — эквипотенциальными линиями, или эквипотенциалями.
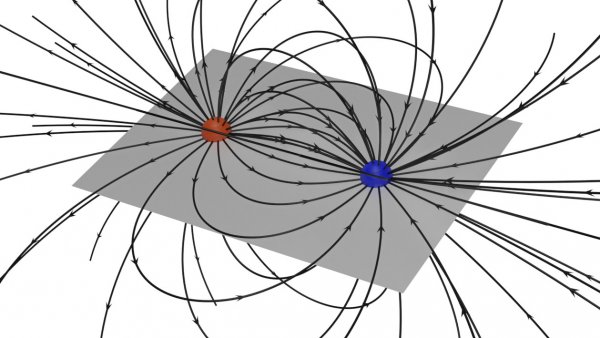
В векторном поле величина, характеризующая это поле в отдельных точках, может быть представлена вектором, начало которого помещается в данную точку. Для наглядного изображения векторного поля прибегают к построению линий, которые проводят так, чтобы касательная в каждой ее точке сов падала с вектором, характеризующим эту точку.
Линии поля, проведенные одна от другой на определенном расстоянии, дают представление о характере распределения поля в пространстве (в области, где линии гуще, значение векторной величины больше, а где линии реже, значение ее меньше).
Безвихревые и вихревые поля
Поля различаются не только по виду физических величин, которые определяют их, но и по характеру, т. е. могут быть либо безвихревыми, состоящими из несмешивающихся параллельных струй (иногда эти поля, называют ламинарными, т. е. слоистыми), либо вихревыми (турбулентными).
Одно и то же безвихревое поле в зависимости от характеризующих его величин может быть как скалярно-потенциальным, так и векторно-безвихревым.
Скалярно-потенциальными будут электростатическое, магнитное и гравитационное поля, если их определять по энергии, распределенной в поле. Однако то же поле (электростатическое, магнитное, гравитационное) является векторным, если характеризуется силами, действующими в нем.
Безвихревое, или потенциальное, поле всегда обладает скалярным потенциалом. Важной особенностью функции скалярного потенциала является ее непрерывность.
Примером безвихревого поля в области электрических явлений является электростатическое поле. Примером вихревого поля является магнитное поле в толще проводника с током.
Существуют так называемые смешанные векторные поля. Примером смешанного поля является магнитное поле вне проводников с током (магнитное поле внутри этих проводников представляет собой вихревое поле).