Аналитическая запись структуры и условий работы релейных схем дает возможность производить аналитические равносильные преобразования схем, т. е. путем преобразования структурных формул находить схемы, аналогичные по своему действию. Особенно полно методы преобразования разработаны для структурных формул, выражающих контактные схемы.
Для контактных схем используется математический аппарат алгебры логики, точнее — одной из наиболее простых ее разновидностей, называющейся исчислением высказываний или булевой алгеброй (по фамилии математика прошлого века Дж. Буля).
Исчисление высказываний первоначально разрабатывалось для исследования зависимости (истинности или ложности сложных суждений от истинности или ложности составляющих их простых суждений. По существу исчисление высказываний представляет собой алгебру двух чисел, т. е. такую алгебру, в которой каждый отдельный аргумент и любая функция могут иметь одно из двух значений.
Этим и определяется возможность использования булевой алгебры для преобразования контактных схем, так как каждый из входящих в структурную формулу аргументов (контактов) может принимать всего два значения, т. е. может быть замкнутым или разомкнутым, и вся функция, представленная структурной формулой, может выражать или замкнутую, или разомкнутую цепь.
Булева алгебра вводит в рассмотрение:
1) объекты, которые, как и в обычной алгебре, носят названия: независимые переменные и функции, – однако, в отличие от обычной алгебры, в булевой алгебре и те, и другие могут принимать только два значения: 0 и 1;
2) основные логические операции:
-
логическое сложение (или дизъюнкцию, логическое ИЛИ, обозначается знаком ?), которое определяется так: результат операции равен 0 тогда и только тогда, когда все аргументы операции равны 0, в остальных случаях результат равен 1;
-
логическое умножение (или конъюнкцию, логическое И, обозначается знаком ?, или не обозначается вовсе), которое определяется так: результат операции равен 1 тогда и только тогда, когда все аргументы операции равны 1, в остальных случаях результат равен 0;
-
отрицание (или инверсию, логическое НЕ, обозначается чертой над аргументом), которое определяется так: результат операции имеет значение, противоположное значению аргумента;
3) аксиомы (законы булевой алгебры), определяющие правила преобразования логических выражений.
Отметим, что каждая из логических операций может выполняться как над переменными, так и над функциями, которые в дальнейшем будем называть булевыми функциями. Напомним, что по аналогии с обычной алгеброй в булевой алгебре операция логического умножения имеет приоритет перед операцией логического сложения.
Логические выражения образуется путем объединения знаками логических операций ряда объектов (переменных или функций), называемых аргументами операции.
Преобразование логических выражений с помощью законов булевой алгебры выполняется обычно с целью его минимизации, так как чем проще выражение, тем меньше сложность логической схемы, являющейся технической реализацией логического выражения.
Законы булевой алгебры представляются в виде совокупности аксиом и следствий. Они проверяются довольно просто с помощью подстановки различных значений переменных.
Техническим аналогом любого логического выражения для булевой функции является логическая схема. При этом переменные, от которых зависит булева функция, связываются с внешними входами этой схемы, значение булевой функции формируется на внешнем выходе схемы, а каждая логическая операция в логическом выражении реализуется логическим элементом.
Таким образом, для каждого набора входных сигналов на выходе логической схемы формируется сигнал, соответствующий значению булевой функции на данном наборе переменных (в дальнейшем будем использовать такое соглашение: 0 – низкий уровень сигнала, 1 – высокий уровень сигнала).
При построении логических схем будем считать, что переменные подаются на вход в парафазном коде (то есть доступно и прямое, и инверсное значение переменной).
В табл. 1 приведены условные графические обозначения некоторых логических элементов по ГОСТ 2.743-91, а также их зарубежные аналоги.
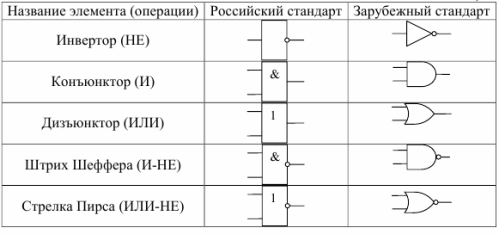
Кроме элементов, реализующих три операции булевой алгебры (И, ИЛИ, НЕ), в табл. 1 приведены и элементы, реализующие операции производные от основных:
- И-НЕ – отрицание логического умножения, также называется штрих Шеффера (обозначается |)
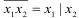
- ИЛИ-НЕ – отрицание логического сложения, также называется стрелка Пирса (обозначается ?)
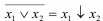
Последовательно соединяя логические элементы между собой, можно реализовать любую булеву функцию.
Структурные формулы, выражающие релейные схемы в целом, т. е. содержащие символы реагирующих орланов, нельзя рассматривать как функции двух значений, выражающих только замкнутую или разомкнутую цепи. Поэтому при оперировании такими функциями возникает ряд новых зависимостей, выходящих за пределы булевой алгебры.
В булевой алгебре существуют четыре пары основных законов: два переместительных, два сочетательных, два распределительных и два законна инверсии. Эти законы устанавливают равносильность различных выражений, т. е. рассматривают такие выражения, которые можно взаимно заменить подобно замене для тождеств в обычной алгебре. В качестве символа равносильности примем символ, одинаковый с символом равенства в обычной алгебре (=).
Справедливость законов булевой алгебры для контактных схем будем устанавливать путем рассмотрения схем, соответствующих левым и правым частям равносильных выражений.
Переместительные законы
Относительно сложения: х + у = у + х
Соответствующие этим выражениям схемы представлены на рис. 1,а.
Левая и правая схемы представляют нормально разомкнутые цепи, каждая из которых при срабатыванию любого из элементов (X или Y) замыкается, т. е. эти схемы равносильны. Относительно умножения: х ·у = у ·х.
Соответствующие этим выражениям схемы представлены на рис. 1,б, их равносильность также очевидна.
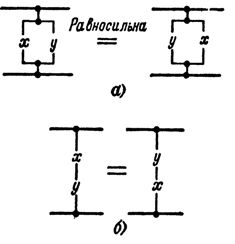
Рис. 1
Сочетательные законы
Относительно сложения: (x + y) + z = x + (y + z)
Относительно умножения: (x ·y) ·z = x ·(y ·z)
Соответствующие этим выражениям пары равносильных схем представлены на рис. 2,а, б
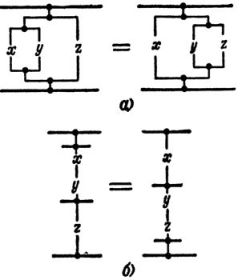
Рис. 2
Распределительные законы
Умножения относительно сложения: (х + у) +z = х + (y + z)
Сложения относительно умножения. x ·y + z = (x + z) ·(y +z )
Соответствующие этим выражениям схемы представлены на рис. 3,а, б.
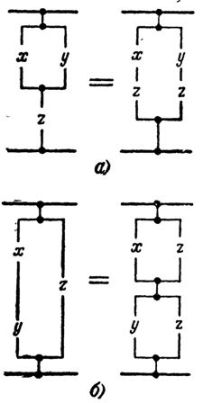
Рис. 3.
В равносильности этих схем можно легко убедиться, рассмотрев различные комбинации срабатывания контактов.
Законы инверсии
Относительно сложения: х + у = х·у
Черта над левой частью выражения является знаком отрицания или инверсии. Этот знак указывает на то, что вся функция имеет обратное значение но отношению к выражению, стоящему под знаком отрицания. Начертить схему, соответствующую всей инверсной функции, не представляется возможным. Однако может быть начерчена схема, соответствующая выражению, стоящему под знаком отрицания. Таким образом, формула может быть иллюстрирована схемами, представленными на рис. 4,а.
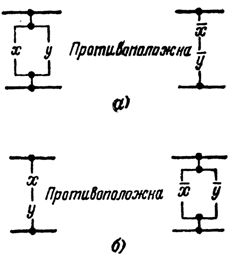
Рис. 4.
Левая схема соответствует выражению х + у, а правая — х ·у
Эти две схемы противоположны друг другу по действию, а именно: если левая схема при невозбужденных элементах X, Y представляет собой разомкнутую цепь, то правая — замкнутую. Если в левой схеме при срабатывании любого из элементов цепь замыкается, то в правой, наоборот, размыкается.
Так как в соответствии с определением знака отрицания функция х + у противоположна функции х + у, то очевидно, что х + у = х·у.
Относительно умножения: х · у = х + у
Соответствующие схемы представлены на рис. 4,б.
Переместительные и сочетательные и законы и распределительный закон умножения относительно сложения (соответствуют аналогичным законам обычной алгебры). Поэтому в случае преобразования структурных формул в отношении порядка сложения и умножения членов, вынесения членов за скобки и раскрытия скобок можно следовать правилам, установленным для обращения с обычными алгебраическими выражениями. Распределительный закон сложения относительно умножения и законы инверсии являются специфическими для булевой алгебры.