Структура, конструкция, принцип действия различных автоматов в значительной мере определяются его функциональным назначением. Различают технологические, транспортные, вычислительные, военные и другие автоматы. В различных отраслях промышленности широко внедряются целые автоматические комплексы, предназначенные для выполнения сложных технологических процессов. Разрабатываются и строятся автоматы, реализующие разнообразные логические функции (Логические машины).
Теория автоматов — раздел кибернетики, возникший под влиянием запросов техники цифровых вычислительных и управляющих машин. Дискретные автоматы, изучаемые в теории автоматов, являются абстрактными моделями реальных систем (как технических, так и биологических), которые перерабатывают дискретную (цифровую) информацию дискретными временными тактами.
В основе теории автоматов лежат точные математические понятия, формализующие интуитивные представления о функционировании (поведении) автомата и о его структуре (внутреннем устройстве).
При этом под преобразованием информации всегда понимается операция, преобразующая последовательности входные, составленные из букв входного алфавита, в последовательности выходные, составленные из букв выходного алфавита.
Широко применяется аппарат математической логики, алгебры, теории вероятностей, комбинаторики и теории графов.
Проблематика теории автоматов в некоторой своей части (структурная теория автоматов) выросла из теории релейно-контактных схем, которая начала складываться в конце 1930-х гг. с привлечением методов алгебры логики.
В структурной теории автоматов исследуются различного рода схемы, предназначаемые для описания того, как сложный автомат создается из более простых компонент (элементов), надлежащим образом соединенных в единую систему.
Другое направление, называемое абстрактной теории автоматов, изучает поведение автоматов (т. е. характер осуществляемого ими преобразования информации) при отвлечении от специфики их внутреннего устройства и возникло в 1950-х гг.
В рамках абстрактной теории автоматов содержание понятий «автомат» и «машина» исчерпывается, по существу, стандартным описанием того преобразования информации, которое осуществляется автоматом. Такое преобразование может быть детерминированным, но может иметь и вероятностную природу.
Наиболее изученными являются детерминированные машины (автоматы), к которым относятся конечные автоматы — главный объект изучения в теории автоматов.
Конечный автомат характеризуется конечностью объема памяти (числа внутренних состояний) и задается посредством функции перехода. При некоторой целесообразной идеализации все современные математические машины и даже мозг, с точки зрения их функционирования, можно рассматривать как конечные автоматы.
Термины «последовательностная машина», «автомат Мили», «автомат Мура» употребляются в литературе (причем не одинаково всеми авторами) как синонимы термина «конечный автомат» либо для подчеркивания тех или иных особенностей в функциях перехода конечного автомата.
К автоматам с неограниченной памятью относится машина Тьюринга, способная осуществлять (потенциально) любое эффективное преобразование информации. Понятие «машина Тьюринга» возникло раньше понятия «конечный автомат» и изучается преимущественно в теории алгоритмов.
Абстрактная теория автоматов тесно связана с известными алгебраическими теориями, например с теорией полугрупп. С прикладной точки зрения представляют интерес результаты, которые характеризуют преобразование информации в автомате в терминах его объема памяти.
Так, например, обстоит дело в задачах с экспериментами над автоматами (работы Э. Ф. Мура и др.), в которых по результатам экспериментов получаются те или иные сведения о функциях перехода автомата или об его объеме памяти.
Другая задача заключается в оценке периодов выходных последовательностей, исходя из имеющихся сведений об объеме памяти автомата и о периодах входных последовательностей.
Большое значение имеют разработка приемов минимизации памяти конечных автоматов и исследование их поведения в случайных средах.
В абстрактной теории автоматов проблема синтеза заключается в следующем. В терминах некоторого четко формализованного языка записываются условия, предъявляемые к поведению проектируемого автомата (к событию, представимому в автомате). При этом требуется выработать методы, которые по любому записанному условию:
1) выясняют, существует ли такой конечный автомат, что осуществляемое им преобразование информации удовлетворяет этому условию;
2) если да, то строят функции перехода такого конечного автомата или же оценивают его объем памяти.
Решение проблемы синтеза в такой постановке предполагает предварительное создание удобного языка для записи условий работы автомата с удобными алгоритмами перехода от записи к переходным функциям.
В структурной теория автоматов проблема синтеза заключается в построении из элементов заданного типа схемы, которая реализует конечный автомат, заданный своими функциями перехода. При этом обычно выдвигают некоторый критерий оптимальности (например, минимальность числа элементов) и стремятся получить оптимальную схему.
Как выяснилось впоследствии, значит, часть методов и понятий, выработанных ранее применительно к релейно-контактным схемам, применима и для схем других типов.
В связи с развитием электронной техники наибольшее распространение нашли схемы из функциональных элементов (логические сети). Частным случаем логических сетей являются абстрактные нервные сети, элементы которых называются нейронами.
Разработано много методов синтеза в зависимости от типа схем и от преобразования информации, для реализации которого они предназначены (Синтез релейных устройств).
Смотрите — Минимизация комбинационных схем, карты Карно, синтез схем
Конечный автомат — математическая модель управляющей системы с фиксированным (не способным к увеличению в процессе работы) размером памяти.
Понятие конечный автомат является математической абстракцией, характеризующей общие черты множества управляющих систем (например, многотактного релейного устройства). У всех таких систем имеются общие признаки, которые естественно принять в качестве определения конченого автомата.
Всякий конченый автомат имеет вход, подвергающийся внешним воздействиям, и внутренние элементы. Как для входа, так и для внутренних элементов существует фиксированное число дискретных состояний, которые они способны принимать.
Изменение состояний входа и внутренних элементов происходит в дискретные моменты времени, интервалы между которыми называются тактами. Внутреннее состояние (состояние внутренних элементов) в конце такта полностью определено внутренним состоянием и состоянием входа в начале такта.
К указанной характеристике могут быть сведены все другие определения конченого автомата, в частности определения, предполагающие у конченого автомата наличие выхода, зависящего от внутреннего состояния автомата в данный момент.
С точки зрения такой характеристики, для описания конченого автомата не имеет никакого значения природа его входов и внутренних состояний. Можно вместо входов и состояний рассматривать просто их номера в произвольно выбранной нумерации.
Конечный автомат будет задан, если будет указана зависимость номера его внутреннего состояния от номера предыдущего внутреннего состояния и номера предыдущего состояния входа. Такое задание может иметь вид конечной таблицы.
Другой распространенный способ задания конченого автомата — построение т. н. диаграммы переходов. Состояния входа часто называются просто входами, а внутреннего состояния — просто состояниями.
Конечный автомат может быть моделью как технических устройств, так и некоторых биологических систем. Автоматы первого типа являются, например, релейные устройства и различные электронные вычислительные машины, в т. ч. программируемые логические контроллеры.
В случае релейного устройства роль состояний входа играют комбинации состояний воспринимающих элементов релейного устройства (каждая комбинация таких состояний представляет собой «сложное состояние», характеризуемое указанием для всех воспринимающих элементов тех дискретных состояний, которые они имеют в данный момент). Аналогично, комбинации состояний промежуточных элементов релейного устройства играют роль внутренних состояний.
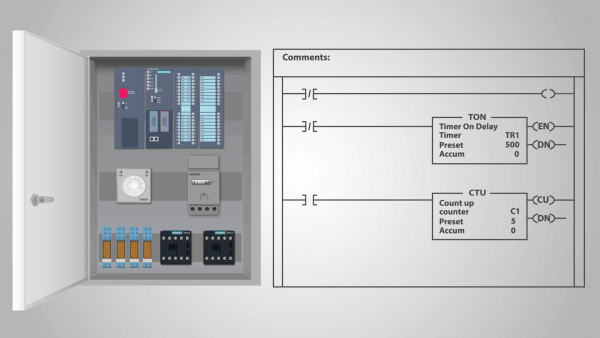
Программируемый логический контроллер (ПЛК) представляет собой пример устройства релейного действия, которое может быть названо автономным конечным автоматом.
Действительно, после того как в ПЛК введена программа и контроллер начал вычисление, она не подвергается внешним воздействиям, причем каждое ее последующее состояние полностью определено ее предыдущим состоянием. Можно считать, что вход в каждом такте имеет одно и то же состояние.
Обратно, всякий конечный автомат, имеющий единственное возможное состояние входа, естественно называть автономным, поскольку в этом случае внешняя среда не несет информации, управляющей его поведением.
Смотрите также:
Применение микропроцессорных систем в электротехнике на примере использования ПЛК