В практической инженерной работе под логическим синтезом понимают процесс составления собственных функций конечного автомата, работающего по заданному алгоритму. В результате этой работы должны быть получены алгебраические выражения для выходных и промежуточных переменных, на основе которых могут быть построены схемы, содержащие минимальное количество элементов. В результате синтеза можно получить несколько равносильных вариантов логических функций, алгебраические выражения которых удовлетворяют принципу минимальности элементов.
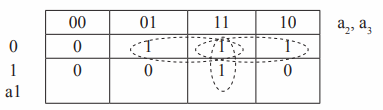Рис. 1. Карта Карно
Процесс синтеза схем сводится главным образом к составлению таблиц истинности или карт Карно по заданным условиям появления и исчезновения выходных сигналов. Способ задания логической функции с помощью таблиц истинности неудобен при большом количестве переменных. Значительно проще логические функции задавать при помощи карт Карно.
Карта Карно представляет собой четырехугольник, разделенный на элементарные квадраты, каждому из которых соответствует своя комбинация значений всех входных переменных. Число клеток равно числу всех наборов входных переменных – 2n, где n – число входных переменных.
Обозначения входных переменных пишутся сбоку и сверху карты, а значения переменных записываются в виде ряда (или столбца) двоичных чисел сверху над каждым столбцом карты (или сбоку против каждой строки карты) и относятся ко всей строке или столбцу (см. рисунок 1). Ряд двоичных чисел записывается так, чтобы соседние значения отличались только у одной переменной.
Например, для одной переменной – 0,1. Для двух переменных – 00, 01, 11, 10. Для трех переменных – 000, 001, 011, 010, 110, 111, 101, 100. Для четырех переменных – 0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100, 1100, 1101, 1111, 1110, 1010, 1011, 1001, 1000. В каждом квадрате записывается значение выходной переменной, соответствующее комбинации входных переменных для данной клетки.
Карту Карно можно строить по словесному описанию алгоритма, по графсхеме алгоритма, а также непосредственно по логическим выражениям функции. При этом заданное логическое выражение должно быть приведено к форме СДНФ (совершенной дизъюнктивной нормальной форме), под которой понимается форма логического выражения в виде дизъюнкции элементарных конъюнкций, имеющих полный набор входных переменных.
Логическое выражение содержит конъюнкции только единичных конституентов, поэтому каждому набору переменных в конъюнкциях должна быть поставлена единица в соответствующей клетке карты Карно, в остальных клетках ставится ноль.
В качестве примера минимизации и синтеза комбинационной схемы рассмотрим работу упрощенной транспортной системы. На рис. 2 представлена транспортная система с бункером, которая состоит из конвейера 1 с датчиком наличия скольжения (ДНС), расходного бункера 4 с датчиком верхнего уровня (ДВУ), затвора 3 и реверсивного конвейера 2 с датчиками наличия материала на ленте (ДНМ1 и ДНМ2).
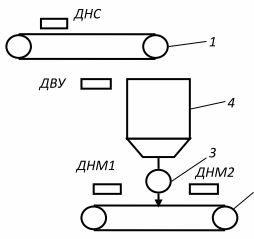
Рис. 2. Транспортная система
Составим структурную формулу включения аварийного реле в случае:
1) проскальзывания конвейера 1 (сигнал датчика ДНС);
2) переполнения накопительного бункера 4 (сигнал датчика ДВУ);
3) при включенном затворе отсутствие материала на ленте реверсивного конвейера (отсутствие сигналов с датчиков наличия материала (ДНМ1 И ДНМ2).
Обозначим элементы входных переменных буквами:
-
Сигнал ДНС - а1.
-
Сигнал ДВУ - а2.
-
Сигнал концевого выключателя затвора - а3.
-
Сигнал ДНМ1 - а4.
-
Сигнал ДНМ2 - а5.
Таким образом, имеем пять входных переменных и одну выходную функцию Р. Карта Карно будет иметь 32 клетки. Клетки заполняются на основании условий работы аварийного реле. Те клетки, в которых значения переменных а1 и а2 по условию равны единице, заполняются единицами, т.к. сигнал с этих датчиков должен включить аварийное реле. Единицы также проставляются в клетки по третьему условию, т.е. когда при открытом затворе, на реверсивном конвейере отсутствует материал.
Для минимизации функции в соответствие с ранее указанными свойствами карт Карно очерчиваем контурами ряд единиц, являющихся по определению соседними клетками. У контура, охватывающего вторую и третью строчки карты, все переменные, кроме а1, меняют свои значения. Следовательно, функция этого контура будет состоять только из одной переменой а1.
Аналогично функция второго контура, охватывающего третью и четвертую строчки, будет состоять только из переменной а2. Функция третьего контура, охватывающего последний столбец карты, будет состоять из переменных а3, а4 и а5, так как переменные а1 и а2 в этом контуре меняют свои значения. Таким образом, функции алгебры логики данной системы имеет следующий вид:
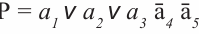
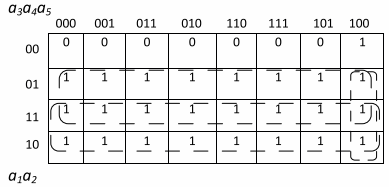
Рис. 3. Карта Карно для транспортной схемы
На рисунке 3 приведены схемы реализации данной ФАЛ на релейноконтактных элементах и на логических элементах.
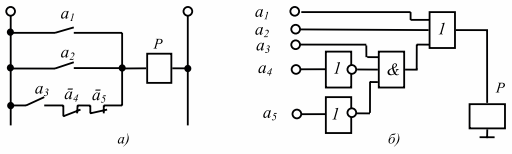
Рис. 4. Принципиальная схема управления аварийным реле транспортной системы: а – релейно-контактная схема; б – на логических элементах
Кроме карты Карно, есть и другие методы минимизации функции алгебры логики. В частности существует метод непосредственного упрощения аналитического выражения функции, заданной в СДНФ.
В этой форме можно найти конституенты, отличающиеся значением одной переменной. Такие пары конституентов тоже называются соседними, и в них функция тоже, как и в карте Карно, не зависит от переменной, изменяющей свое значение. Поэтому, применив закон склеивания, можно сократить выражение на одну конъюнкцию.
Проделав такое преобразование со всеми соседними парами, можно избавиться от повторяющихся конъюнкций, применив закон идемпотенции. Полученное выражение называется сокращенной нормальной формой (СНФ), а конъюнкции, входящие в СНФ, называются импликатами. Если к функции приемлемо применение закона обобщенного склеивания, то функция будет еще меньше. После всех приведенных преобразований функция называется тупиковой.
Синтез логических структурных схем
В инженерной практике часто приходится в целях совершенствования оборудования переходить от релейно-контакторных схем к бесконтактным на основе логических элементов, оптронов и тиристоров. Для осуществления такого перехода может быть использована следующая методика.
После анализа релейно-контакторной схемы проводится разделение всех сигналов, действующих в ней на входные, выходные и промежуточные, и вводятся для них буквенные обозначения. К входным сигналам относятся сигналы о состоянии конечных и путевых выключателей, кнопок управления, универсальных переключателей (кулачковых контроллеров), датчиков, контролирующих технические параметры, и т.п.
Выходные сигналы управляют исполнительными элементами (магнитными пускателями, электромагнитами, сигнальными устройствами). Промежуточные сигналы появляются при срабатывании промежуточных элементов. К ним относятся реле различных назначений, например, реле времени, реле выключения механизмов, реле сигнализации, реле выбора режима работы и т.д. Контакты этих реле, как правило, входят в цепи выходных или других промежуточных элементов. Промежуточные сигналы подразделяются на сигналы без обратных связей и с обратными связями. Первые в своих цепях имеют только входные переменные, вторые имеют сигналы входных, промежуточных и выходных переменных.
Далее записываются алгебраические выражения логических функций для цепей всех выходных и промежуточных элементов. Это наиболее ответственный момент в проектировании бесконтактной системы автоматического управления. Функции алгебры логики составляются для всех реле, контакторов, электромагнитов, сигнальных устройств, которые включены в схему управления релейно-контакторного варианта.
Релейно-контакторные устройства в силовой цепи оборудования (тепловые реле, реле максимального тока, автоматические выключатели и др.) функциями логики не описываются, так как эти элементы в соответствие со своими функциями логическими элементами заменены быть не могут. Если имеются бесконтактные варианты этих элементов, то они могут быть включены в логическую схему управления своими вы- ходными сигналами, которые должны учитываться алгоритмом управления.
По полученным структурным формулам в нормальных формах может быть построена структурная схема на логических элементах в булевом базисе (И, ИЛИ, НЕ). При этом следует руководствоваться принципом минимума элементов и корпусов микросхем логических элементов. Для этого следует подобрать такую серию логических элементов, чтобы она полностью могла по минимуму реализовать все структурные функции алгебры логики. Часто для этих целей подходит логика «ЗАПРЕТ», «ИМПЛИКАЦИЯ».
При построении логических устройств обычно не пользуются функционально полной системой логических элементов, реализующих все основные логические операции. На практике, с целью сокращения номенклатуры элементов, пользуются системой элементов, включающих только два элемента, выполняющих операции И-НЕ (штрих Шеффера) и ИЛИ-НЕ (стрелка Пирса) или даже только один из этих элементов. Причем число входов этих элементов, как правило, задано. Поэтому вопросы синтеза логических устройств в заданном базисе логических элементов имеют большое практическое значение.