В середине XIX века ирландский математик Джордж Буль разработал алгебру логики («Исследование законов мышления»). Поэтому алгебру логики называют также булевой алгеброй.
Давая высказываниям буквенные обозначения, выражая операции логических преобразований в символах действий и пользуясь установленными для этих действий правилами и аксиомами, алгебра логики позволяет процесс рассуждений при решении задачи, заданной в условиях логики высказываний, полностью описать в алгоритмах, т. е. иметь математически записанную программу решения данного вопроса.

Для обозначения истинности или ложности высказываний (т. е. для введения значений оценки высказываний) алгебра логики пользуется удобной в данном случае двоичной системой. Если высказывание истинно, оно принимает значение 1, если ложно — 0. В отличие от двоичных чисел, логические 1 и 0 выражают не количество, а состояние.
Так, в электрических схемах, описанных с помощью булевой алгебры, где 1 — наличие напряжения, а 0 — отсутствие его, подача напряжений от нескольких источников в один узел схемы (т. е. поступление на него нескольких логических единиц) отображается также логической единицей, которая указывает не на суммарное напряжение в узле, а только на наличие его.
При описании входных и выходных сигналов логических схем используются переменные, которые принимают значения только логического 0 или 1. Зависимость выходных сигналов от входных определяется логической операцией (функцией). Обозначим входные переменные Х1 и Х2, а выходную, полученную путем логической операции над ними — у.
Рассмотрим три основные элементарные логические операции, с помощью которых могут быть описаны все более сложные.
1. Операция ИЛИ — логическое сложение:
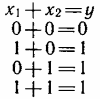
Рассматривая все возможные значения переменных, можно определить операцию ИЛИ, как достаточность хотя бы одной единицы на входе для получения единицы на выходе. Название операции объясняется смысловым значением союза ИЛИ во фразе: «Если ИЛИ один вход, ИЛИ второй — единицы, то выход — единица».
2. Операция И — логическое умножение:
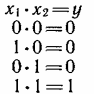
Из рассмотрения полного набора значений переменных операция И определяется, как необходимость совпадения всех единиц на входах для получения единицы на выходе: «Если И один вход, И второй — единицы, то выход— единица».
3. Операция НЕ — логическое отрицание или инверсия. Обозначается чертой над переменной.
При инверсии значение переменной заменяется на обратное.
Основные законы алгебры логики:
1. Закон нулевого множества: произведение любого числа переменных обращается в нуль, если какая-либо одна из переменных имеет значение нуль, независимо от значений других переменных:
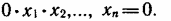
2. Закон универсального множества — сумма любого числа переменных обращается в единицу, если хотя бы одна из переменных имеет значение единицы, независимо от других переменных:
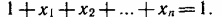
3. Закон повторения — повторяющиеся переменные в выражении могут быть опущены (иначе говоря, в алгебре Буля возведения в степень и умножения на числовой коэффициент нет):
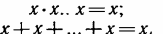
4. Закон двойной инверсии — дважды выполненная инверсия является пустой операцией:
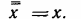
5. Закон дополнительности — произведение любой переменной и ее инверсии есть нуль:
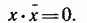
6. Сумма любой переменной и ее инверсии есть единица:
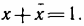
7. Переместительные законы — результат выполнения операций умножения и сложения не зависит от того, в каком порядке следуют переменные:
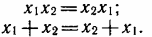
8. Сочетательные законы — при операциях умножения и сложения переменные можно группировать в любом порядке:
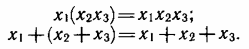
9. Распределительные законы — допускается вынесение общего множителя за скобки:
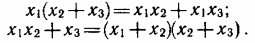
10. Законы поглощения — указывают способы упрощения выражений при участии переменной во всех сомножителях и слагаемых:
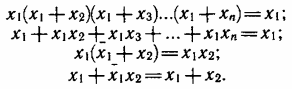
11. Законы де Моргана — инверсия произведения есть сумма инверсий переменных:
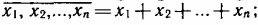
инверсия суммы есть произведение инверсий переменных:
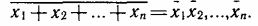




 Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное:
Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное: