 Системой счисления называют совокупность правил представления чисел с помощью различных цифровых - знаков. Системы счисления подразделяются на два типа: непозиционные и позиционные.
Системой счисления называют совокупность правил представления чисел с помощью различных цифровых - знаков. Системы счисления подразделяются на два типа: непозиционные и позиционные.
В непозиционных системах счисления значение любой цифры не зависит от занимаемой ею позиции, т. е. от занимаемого места в совокупности цифр. В римской системе счисления имеется всего семь цифр: единица (I), пять (V), десять (X), пятьдесят (L), сто (С), пятьсот (D), тысяча (М). С помощью этих чисел (символов) остальные числа записываются с применением сложения и вычитания. Например, IV есть запись числа 4 (V - I), VI - числа 6 (V + I) и т. д. Число 666 записывается в римской системе так: DCLXVI.
Эта форма записи менее удобна, чем та, которой мы пользуемся в настоящее время. Здесь шесть единиц записываются одним символом (VI), шесть десятков - другим (LХ), шесть сотен - третьим (DC). С числами, записываемыми в римской системе счисления, очень трудно производить арифметические действия. Также общим недостатком непозиционных систем является сложность представления в них достаточно больших чисел, так при этом получается чрезвычайно громоздкая запись.
Теперь рассмотрим то же число 666 в позиционной системе счисления. В нем один знак 6 обозначает число единиц, если он находится на последнем месте, число десятков - если на предпоследнем, и число сотен, если он стоит на третьем месте от конца. Такой принцип записи чисел называется позиционным (поместным). При такой записи каждая цифра получает числовое значение не только в зависимости от своего начертания, но и от того, на каком месте она стоит при записи числа.
В позиционной системе счисления любое число, изображенное в виде А = +а1а2а3 ... an-1an, может быть представлено в виде суммы
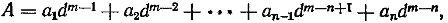
где n - конечное количество разрядов в изображении числа, аi цифра i-гo разряда, d - основание системы счисления, i - порядковый номер разряда, dm-i - «вес» i-ro разряда. Цифры ai должны удовлетворять неравенству 0 <= а <= (d - 1).
Для десятичной системы счисления d = 10 и ai = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Так как цифры, состоящие из единиц и нулей, могут восприниматься как десятичные или двоичные числа, то при их совместном применении обычно указывается основание системы счисления, например (1100)2-двоичная система, (1100)10-десятичная.
В цифровых ЭВМ широко применяются системы, отличные от десятичной: двоичная, восьмеричная и шестнадцатеричная.
Двоичная система счисления
Для этой системы d = 2, и здесь допускается существование только двух цифр, т. е. ai = 0 или 1.
Любое число, выраженное в двоичной системе, представляется в виде суммы произведения степеней основания два, умноженных на двоичную цифру данного разряда. Например, число 101,01 можно записать так: 101,01 = 1х22 + 0х21 + 1х20 + 0х2-1 + 1х2-2, что соответствует числу в десятичной системе: 4 + 1 + 0,25 = 5,25.
В большинстве современных цифровых ЭВМ двоичную систему счисления используют для представления чисел в машине и выполнения над ними арифметических операций.
Двоичная система счисления по сравнению с десятичной позволяет упростить схемы и конструкции арифметического и запоминающего устройства, повысить надежность ЭВМ. Цифра каждого разряда двоичного числа представляется состояниями «включено-выключено» таких элементов, как транзисторы, диоды, которые надежно работают в состояниях «включено-выключено». К недостаткам двоичной системы относится необходимость перевода по специальной программе исходных цифровых данных в двоичную систему счисления, а результатов решения - в десятичную.
Восьмеричная система счисления
Эта система имеет основание d == 8. Для изображения чисел используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
Восьмеричную систему счисления используют в ЭВМ как вспомогательную при подготовке задач к решению (в процессе программирования), при проверке работы машины и отладке программы. Эта система дает более короткую запись числа по сравнению с двоичной системой. Восьмеричная система счисления позволяет просто перейти к двоичной системе.
Шестнадцатеричная система счисления
Эта система имеет основание d = 16. Для изображения чисел используется 16 знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F, причем знаки А ... F изображают десятичные числа 10, 11, 12, 13, 14 и 15. Шестнадцатеричное число (1D4F)18 будет соответствовать десятичному 7503, так как (1D4F)18 = 1 х163 + 13 х 162 + 14 х 161+ 15 x 16о = (7503)10
Шестнадцатеричная система счисления позволяет более компактно записывать двоичные цифры по сравнению с их записью в восьмеричной системе счисления. Она находит применение в устройствах ввода и вывода и устройствах изображения порядков чисел некоторых ЭВМ.
Двоично-десятичная система счисления
Представление числа в двоично-десятичной системе осуществляется следующим образом. За основу берут десятичную запись числа, а затем каждую ее цифру (от 0 до 9) записывают в виде четырехразрядного двоичного числа, называемого тетрадой, т. е. для изображения каждой цифры десятичной системы применяют не один знак, а четыре.
Например, десятичное число 647,59 будет соответствовать двоично-десятичному числу 0110 0100 0111, 0101 1001.
Двоично-десятичная система счисления используется как промежуточная система счисления и для кодирования входных и выходных чисел.
Правила перевода одной системы счисления в другую
Обмен информацией между устройствами ЭВМ производится в основном числами, представленными в двоичной системе счисления. Однако пользователю информация выдается числами в десятичной системе счисления, а адресация команд представляется в восьмеричной системе счисления. Отсюда возникает необходимость в процессе работы ЭВМ переводить числа из одной системы в другую. Для этого пользуются следующим общим правилом.
Чтобы перевести целое число из любой системы счисления в другую, необходимо последовательно делить это число на основание новой системы до тех пор, пока не получится частное, меньшее делителя. Число в новой системе следует записывать в виде остатков деления, начиная с последнего, т. е. справа налево.
Например, переведем десятичное число 1987 в двоичную систему счисления:
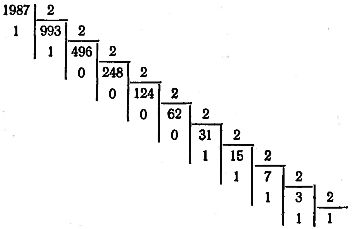
Число 1987 десятичной системы в двоичной системе составит 11111000011, т. е. (1987)10 = (11111000011)2
При переходе от какой-либо системы к десятичной число представляют в виде суммы степеней основания с соответствующими коэффициентами, а затем подсчитывают значение суммы.
Например, переведем восьмеричное число 123 в десятичное: (123)8 = 1 х 82 + 2 х 81 + 3 х 80 = 64 + 16 + 3 = 83, т. е. (123)8 = (83)10
Для перевода дробной части числа из любой системы в другую надо провести последовательное умножение этой дроби и получающихся дробных частей произведения на основание новой системы счисления. Дробная часть числа в новой системе формируется в виде целых частей получающихся произведений, начиная с первого. Процесс умножения продолжают до тех пор, пока не будет вычислено число с заданной точностью.
Например, переведем десятичную дробь 0,65625 в двоичную систему счисления:

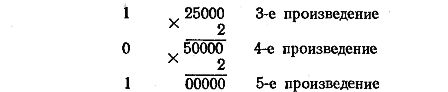
Так как дробная часть 5-го произведения состоит из одних нулей, то дальнейшее умножение является излишним. Это означает, что заданная десятичная дробь переводится в двоичную систему без погрешности, т. е. (0,65625)10 = (0,10101)2.
Перевод из восьмеричной и шестнадцатеричной систем исчисления в двоичную и обратно не сложен. Это объясняется тем, что их основания (d - 8 и d - 16) соответствуют целым степеням двух (23 = 8 и 24 = 16).
Для перевода восьмеричных или шестнадцатеричных чисел в двоичную систему счисления достаточно каждую их цифру заменить соответственно трех или четырехразрядным двоичным числом.
Например, переведем восьмеричное число (571)8 и шестнадцатеричное число (179)16 в двоичную систему счисления.
В обоих случаях получаем одинаковый результат, т. е. (571)8 = (179)16 = (101111001)2
Для перевода числа из двоично-десятичной системы счисления в десятичную необходимо каждую тетраду числа, представленную в двоично-десятичной системе счисления, заменить цифрой, представленной в десятичной системе счисления.
Например, запишем число (0010 0001 1000, 0110 0001 0110)2-10 в десятичной системе счисления, т. е. (0010 0001 1000, 0110 0001 0110)2-10 = (218,625)



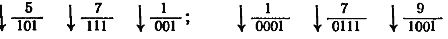
 Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное:
Телеграмм каналы для тех, кто каждый день хочет узнавать новое и интересное: