 Основные условия нагрева и охлаждения электрооборудования рассмотрим на примере однородного проводника, охлаждающегося равномерно со всех сторон.
Основные условия нагрева и охлаждения электрооборудования рассмотрим на примере однородного проводника, охлаждающегося равномерно со всех сторон.
Если через проводник, имеющий температуру окружающей среды, проходит ток, то температура проводника постепенно повышается, так как вся энергия потерь при прохождении тока переходит в тепло.
Скорость нарастания температуры проводника при нагреве током зависит от соотношения между количеством выделяющегося тепла и интенсивностью его отвода, а также теплопоглощающей способности проводника.
Количество тепла, выделенного в проводнике в течение времени dt, будет составлять:
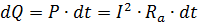
где I — действующее значение тока, проходящего по проводнику, а; Ra — активное сопротивление проводника при переменном токе, ом; Р—мощность потерь, переходящих в тепло, вm. Часть этого тепла идет на нагрев проводника и повышение его температуры, а остальное тепло отводится с поверхности проводника за счет теплоотдачи.
Энергия, идущая на нагрев проводника, равна
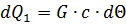
где G — вес токоведущего проводника, кг; с — удельная теплоемкость материала проводника, em•сек/кг•град; Θ — перегрев — превышение температуры проводника по отношению к окружающей среде:
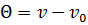
v и vо—температуры проводника и окружающей среды, °С.
Энергия, отводимая с поверхности проводника в течение времени dt за счет теплоотдачи, пропорциональна превышению температуры проводника над температурой окружающей среды:
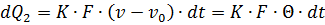
где К — общий коэффициент теплоотдачи, учитывающий все виды теплоотдачи, Вm/см2 °С; F — поверхность охлаждения проводника, см2,
Уравнение теплового баланса за время неустановившегося теплового процесса можно записать в следующем виде:
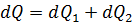
или
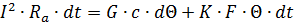
или
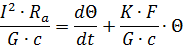
Для условий нормального режима, когда температура проводника изменяется в небольших пределах, можно принять, что R, с, К представляют собой постоянные величины. Кроме того, следует учесть, что до включения тока проводник имел температуру окружающей среды, т. е. начальное превышение температуры проводника над температурой окружающей среды равно нулю.
Решение этого дифференциального уравнения нагрева проводника будет
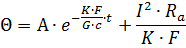
где А — постоянная интегрирования, зависящая от начальных условий.
При t = 0 Θ = 0, т. е. в начальный момент нагреваемый проводник имеет температуру окружающей среды.
Тогда для t = 0 получаем
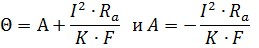
Подставляя значение постоянной интегрирования А, получаем
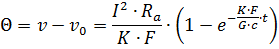
Из этого уравнения следует, что нагрев токоведущего проводника происходят по экспоненциальной кривой (рис. 1). Как видно, с изменением времени подъем температуры проводника замедляется и температура достигает установившегося значения.
Это уравнение дает температуру проводника в любой момент времени t с начала прохождения тока.
Величина установившегося перегрева может быть получена, если в уравнении нагрева принять время t =∞
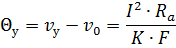
где vу — установившаяся температура поверхности проводника; Θу — установившееся значение превышения температуры проводника над температурой окружающей среды.
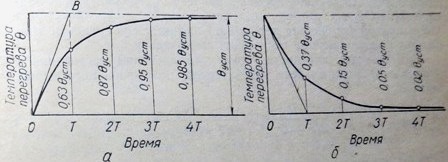
Рис. 1. Кривые нагрева и охлаждения электрооборудования: а — изменение температуры однородного проводника при длительном нагреве; б — изменение температуры при охлаждении
На основании этого уравнения можно написать, что
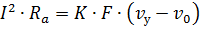
Отсюда видно, что при достижении установившегося режима все выделяющееся в проводнике тепло будет отдаваться в окружающее пространство.
Вводя в основное уравнение нагрева Θу и обозначая через T =Gc/KF получим то же уравнение в более простом виде:
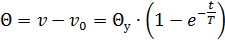
Величина T =Gc/KF называется постоянной времени нагрева и представляет собой отношение теплопоглощающей способности тела к его теплоотдающей способности. Она зависит от размеров, поверхности и свойств проводника или тела и не зависит от времени и температуры.
Для данного проводника или аппарата эта величина характеризует время достижения установившегося режима нагрева и принимается за масштаб измерения времени на диаграммах нагрева.
Хотя из уравнения нагрева следует, что установившийся режим наступает через неограниченно длительное время, на практике время достижения установившейся температуры принимают равным (3—4)•T, так как при этом температура нагрева превышает 98% своего окончательного значения Θу.
Постоянную времени нагрева для простых токоведущих конструкций можно легко вычислить, а для аппаратов и машин она определяется путем тепловых испытаний и последующих графических построений. Постоянная времени нагрева определяется как подкасательная ОТ, построенная по кривой нагрева, а сама касательная ОВ к кривой (от начала координат) характеризует подъем температуры проводника при отсутствии теплоотдачи.
При больших плотностях тока и интенсивном нагревании постоянную времени нагрева рассчитывают по уточненному выражению:
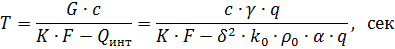
Если предположить, что процесс нагрева проводника происходит без отдачи тепла в окружающее пространство, то уравнение нагрева будет иметь следующий вид:
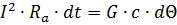
и температура перегрева будет нарастать по линейному закону, пропорционально времени:
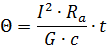
Если в последнее уравнение подставить t =T, то видно, что за период, равный постоянной времени нагрева T =Gc/KF проводник нагревается до установившейся температуры Θу=I2Ra/KF, если за это время не будет происходить теплоотдача.
Величина постоянной времени нагрева для электрического оборудования колеблется от нескольких минут у шин до нескольких часов у мощных трансформаторов и генераторов.
В табл. 1 приводятся значения постоянных времени нагрева для шин некоторых типовых размеров.
При отключении тока прекращается подвод энергии к проводнику, т. е. Pdt=0, поэтому, начиная с момента выключения тока, проводник будет охлаждаться.
Основное уравнение нагрева для этого случая следующее:
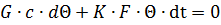
Таблица 1. Постоянные времени нагрева медных и алюминиевых шин
|
Сечение шин, мм* |
Постоянные времени нагрева, мин |
|
|
для меди |
для алюминия |
|
|
25x3 |
7,3 |
5,8 |
|
50x6 |
14,0 |
11,0 |
|
100x10 |
20,0 |
15,8 |
Если охлаждение проводника или оборудования начинается с некоторой температуры перегрева Θу, то решение этого уравнения даст изменение температуры во времени в следующем виде:
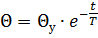
Как видно из рис. 1, б, кривая охлаждения есть та же кривая нагрева, но обращенная выпуклостью вниз (к оси абсцисс).
Постоянная времени нагрева также может быть определена из кривой охлаждения как величина подкасательной, соответствующей любой точке этой кривой.
Рассмотренные выше условия нагрева однородного проводника электрическим током в известной мере распространяются на различное электрооборудование для общей оценки протекания процессов нагрева. Что же касается токоведущих проводников аппаратов, сборных шин и ошиновки, а также других подобных деталей, то полученные выводы позволяют производить необходимые практические расчеты.


