Незатухающие колебания — колебания, энергия которых с течением времени не изменяется. В реальных физических системах всегда существуют причины, вызывающие переход энергии колебаний в тепловую (например, трение в механических системах, активное сопротивление в электрических системах).
Поэтому незатухающие колебания можно получить только при условии, что эти потери энергии восполняются. Такое восполнение автоматически осуществляется в автоколебательных системах за счет энергии из внешнего источника. Электромагнитные незатухающие колебания используются чрезвычайно широко. Для их получения применяются различные генераторы.

Чтобы сделать электрические или механические колебания (колебательного контура или маятника) незатухающими, необходимо все время компенсировать потери на сопротивление или на трение.
Можно, например, воздействовать на колебательный контур переменной ЭДС, которая будет периодически увеличивать ток в катушке, и соответственно поддерживать амплитуду напряжения на конденсаторе. Или можно подталкивать маятник, аналогичным путем поддерживая его гармоническое качание.
Как известно, величина энергии магнитного поля катушки колебательного контура связана с ее индуктивностью и током следующим соотношением (вторая формула — энергия электрического поля конденсатора того же кобательного контура)
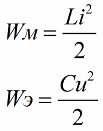
Из первой формулы ясно, что если мы будем периодически увеличивать ток в катушке, воздействуя на контур переменной ЭДС, то (увеличивая или уменьшая второй сомножитель в формуле — ток) станем периодически пополнять тот контур энергией.
Действуя на контур строго в такт его собственным свободным колебаниям, то есть на резонансной частоте, - получим явление электрического резонанса, ведь именно на резонансной частоте колебательная система интенсивне всего поглощает подводимую к ней энергию.
А что, если периодически изменять не второй сомножитель (не ток или напряжение), а первый, - индуктивность или емкость? В этом случае контур тоже испытает изменение своей энергии.
Например, периодически вдвигая и выдвигая сердечник из катушки, или вдвигая и выдвигая из конденсатора диэлектрик, - тоже получим вполне определенное периодическое изменение энергии в контуре.
Запишем это положение для единичного изменения индуктивности катушки:
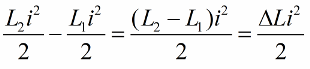
Наиболее выразительным эффект раскачки контура получится в том случае, если изменения индуктивности осуществлять точно вовремя. Например, если взять все тот же контур в произвольный момент времени, когда по нему уже течет какой-то ток i, и внести в катушку сердечник, то энергия изменится на такую величину:
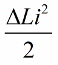
Теперь пусть свободные колебания происходят в контуре сами, но в момент времени, когда через четверть периода энергия полностью перешла в конденсатор и ток в катушке обратился в ноль, резко вынем сердечник из катушки. Индуктивность вернется к своему исходному состоянию, к первоначальной величине L. Работы против магнитного поля при выдвигании сердечника затрачивать не придется. Следовательно при вдвигании сердечника в катушку, контур получил энергию, ибо мы совершили работу, величина которой:
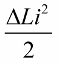
Через четверть периода конденсатор начинает разряжаться, его энергия снова переходит в энергию магнитного поля катушки. Когда магнитное поле достигнет амплитуды — снова резко вдвинем сердечник. Опять индуктивность увеличилась, приросла на ту же величину.
И вновь при нулевом токе возвращаем индуктивность к исходному значению. В итоге, если приросты энергии за каждые полпериода превосходят потери на сопротивление, энергия контура будет все время возрастать, амплитуда колебаний станет увеличиваться. Это положение выражается неравенством:
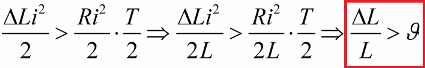
Здесь мы разделили обе части этого неравенства на L, и записали условие возможности параметрического возбуждения скачками для определенной величины логарифмического декремента.
Изменять индуктивность (или емкость) целесообразно два раза за период, следовательно частота изменения параметра (частота параметрического резонанса) должна быть вдвое выше собственной частоты колебательной системы:
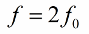
Вот и вырисовался путь возбуждения колебаний в контуре без необходимости изменять непосредственно ЭДС или ток. Начальный флуктуационный ток в контуре так или иначе всегда присутствует, и это даже не принимая во внимание наводки от радиочастотных колебаний в атмосфере.
Если индуктивность (или емкость) будут изменяться не скачками а гармонически, то условие возникновения колебаний станет выглядеть несколько иначе:
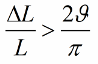
Так как емкость и индуктивность — это параметры контура (как масса маятника или упругость пружины), то и способ возбуждения колебаний получил называние параметрического возбуждения.
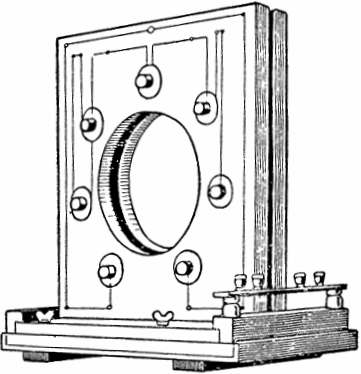
Данное явление открыли и изучали на практике в начале 20 века советские физики Мандельштам и Папалекси. На основе данного физического явления они построили первый параметрический генератор переменного тока мощностью 4 кВт на изменяющейся индуктивности.
В конструкции генератора семь пар плоских катушек располагались по две стороны на каркасе, в полости которого вращался ферромагнитный диск с выступами. Когда диск приводился во вращение мотором, его выступы периодически входили в пространство между каждой парой катушек, и выходили из него, тем самым изменяя индуктивность и возбуждая колебания.
Андрей Повный


