В различных электронных устройствах, например в аппаратуре с электронными и полупроводниковыми приборами, т. е. в усилителях, выпрямителях, радиоприемниках, генераторах, телевизорах, а также в угольных микрофонах, телеграфных аппаратах и во многих других приборах, широко используются пульсирующие токи и напряжения. Чтобы не повторять рассуждения дважды, будем говорить только о токах, но все, что относится к токам, справедливо и для напряжений.
Пульсирующие токи, которые имеют неизменное направление, но меняют свое значение, могут быть различными. Иногда значение тока изменяется от наибольшего значения до наименьшего, не равного нулю. В других случаях ток уменьшается до нуля. Если цепь постоянного тока прерывается с некоторой частотой, то в течение некоторых промежутков времени ток в цепи отсутствует.
На рис. 1 показаны графики различных пульсирующих токов. На рис. 1, а, б изменение токов происходит по синусоидальной кривой, но эти токи не следует считать синусоидальными переменными токами, поскольку направление (знак) тока не изменяется. На рис. 1, в представлен ток, состоящий из отдельных импульсов, т. е. кратковременных «толчков» тока, разделенных друг от друга паузами большей или меньшей длительности, и его часто называют импульсным током. Различные импульсные токи отличаются друг от друга формой и длительностью импульсов, а также частотой их следования.
Пульсирующий ток любого вида удобно рассматривать как сумму двух токов — постоянного и переменного, называемых слагающими, или составляющими, токами. Всякий пульсирующий ток имеет постоянную и переменную составляющие. Многим это кажется странным. Действительно, ведь пульсирующий ток является током, идущим все время в одном направлении и изменяющим свое значение.
Как же можно говорить, что в его составе есть переменный ток, изменяющий свое направление? Однако, если по одному и тому же проводу одновременно пропустить два тока — постоянный и переменный, то оказывается, что в этом проводе будет проходить пульсирующий ток (рис. 2). При этом амплитуда переменного тока не должна превышать значения постоянного тока. Постоянный и переменный токи отдельно по проводу идти не могут. Они складываются в общий поток электронов, имеющий все свойства пульсирующего тока.
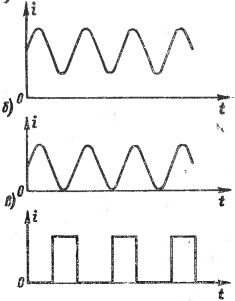
Рис. 1. Графики различных пульсирующих токов
Сложение постоянного и переменного токов можно показать графически. На рис. 2 изображены графики постоянного тока, равного 15 мА и переменного тока с амплитудой 10 мА. Если сложить значения этих токов для отдельных моментов времени, учитывая направления (знаки) токов, то получится график пульсирующего тока, показанный на рис. 2 жирной линией. Этот ток меняется от наименьшего значения 5 мА до наибольшего значения 25 мА.
Рассмотренное сложение токов подтверждает справедливость представления пульсирующего тока как суммы постоянного и переменного токов. Правильность такого представления подтверждается еще и тем, что с помощью некоторых приборов можно отделить друг от друга составляющие этого тока.
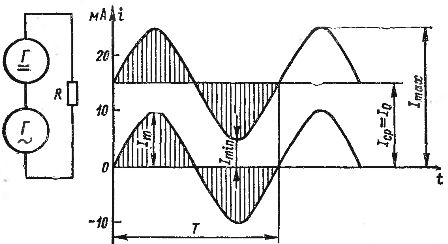
Рис. 2. Получение пульсирующего тока путем сложения постоянного и переменного токов.
Следует подчеркнуть, что любой ток всегда можно представить в виде суммы нескольких токов. Например, ток 5 А можно считать суммой токов 2 и 3 А, протекающих в одном направлении, или суммой токов 8 и 3 А, протекающих в разных направлениях, т. е. иначе говоря, разностью токов 8 и 3 А. Нетрудно подобрать и другие комбинации двух или большего числа токов, дающих в сумме ток 5 А.
Здесь имеется полное сходство с принципом сложения и разложения сил. Если на какой-либо предмет действуют две одинаково направленные силы, то их можно заменить одной суммарной силой. Силы, действующие в противоположных направлениях, можно заменить одной разностной силой. И, наоборот, данную силу всегда можно считать суммой соответствующих одинаково направленных сил, или разностью противоположно направленных сил.
Постоянный или синусоидальный переменный ток нет необходимости разлагать на составные токи. Если же заменить пульсирующий ток суммой постоянного и переменного токов, то, применяя к этим составляющим токам известные законы постоянного и переменного токов, можно решать многие вопросы и делать необходимые расчеты, относящиеся к пульсирующему току.
Понятие о пульсирующем токе как о сумме постоянного и переменного токов является условным. Нельзя, конечно, считать, что в некоторые промежутки времени по проводу действительно протекают навстречу друг другу постоянный и переменный токи. Никаких двух встречных потоков электронов на самом деле нет.
В действительности пульсирующий ток представляет собой единый ток, изменяющий свое значение во времени. Более правильно говорить о том, что пульсирующее напряжение или пульсирующая ЭДС могут быть представлены в виде суммы постоянной и переменной составляющих.
Например, на рис. 2 показано как складываются алгебраически постоянная ЭДС одного генератора с переменной ЭДС другого генератора. В результате имеем пульсирующую ЭДС, вызывающую соответствующий пульсирующий ток. Однако, можно условно считать, что постоянная ЭДС создает в цепи постоянный ток, а переменная ЭДС — переменный ток, которые, складываясь, образуют пульсирующий ток.
Каждый пульсирующий ток можно характеризовать максимальным и минимальным значениями Iтах и Iтin, а также его постоянной и переменной составляющими. Постоянная составляющая обозначается I0. Если переменная составляющая является синусоидальным током, то ее амплитуду обозначают Iт (все эти величины показаны на рис. 2).
Не следует смешивать друг с другом Iт и Iтах. Также не следует называть амплитудой максимальное значение пульсирующего тока Iтах. Понятие амплитуды принято относить только к переменным токам. Применительно к пульсирующему току можно говорить лишь об амплитуде его переменной составляющей.
Постоянная составляющая пульсирующего тока может быть названа его средним значением Iср, т. е. средним арифметическим. Действительно, если рассмотреть изменения за один период пульсирующего тока, показанного на рис. 2, то хорошо видно следующее: за первый полупериод к току 15 мА добавляется ряд значений переменкой составляющей тока, изменяющихся от 0 до 10 мА и опять до 0, а во время второго полупериода точно такие же значения тока вычитаются из тока 15 мА.
Следовательно, ток 15 мА действительно является средним значением. Поскольку ток представляет собой перенос электрических зарядов через поперечное сечение провода, то Iср есть значение такого постоянного тока, который за один период (или за целое число периодов) переносит такое же количество электричества, как и данный пульсирующий ток.
У синусоидального переменного тока значение Iср за период равно нулю, так как количество электричества, прошедшее, через поперечное сечение провода за один полупериод, равно количеству электричества, которое проходит в обратном направлении за другой полупериод. На графиках токов, показывающих зависимость тока i от времени t, количество электричества, переносимое током, выражается площадью фигуры, ограниченной кривой тока, так как количество электричества определяется произведением it.
Для синусоидального тока площади положительной и отрицательной полуволн равны. У пульсирующего тока, показанного на рис.2, в первый полупериод к количеству электричества, переносимому током Iср, добавляется количество электричества, переносимое переменной составляющей тока (заштрихованная площадь на рисунке). А во второй полупериод точно такое же количество электричества вычитается. В результате за целый период переносится такое же количество электричества, как при одном постоянном токе Iср, т. е. площадь прямоугольника Iср Т равна площади, ограниченной кривой пульсирующего тока.
Таким образом, постоянная составляющая, или среднее значение тока, определяется переносом электрических зарядов через поперечное сечение провода.
Уравнение тока, показанного на рис. 2, очевидно должно быть написано в следующем виде:
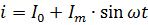
Мощность пульсирующего тока следует вычислять как сумму мощностей составляющих его токов. Например, если ток, показанный на рис.2, проходит через резистор сопротивлением R, то его мощность
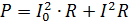
где I = 0,7Im — действующее значение переменной составляющей.
Можно ввести понятие о действующем значении пульсирующего тока Iд. Мощность при этом вычисляется обычным способом:
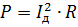
Приравнивая это выражение к предыдущему и сокращая на R, получим:
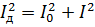
Такие же соотношения могут быть получены и для напряжений.