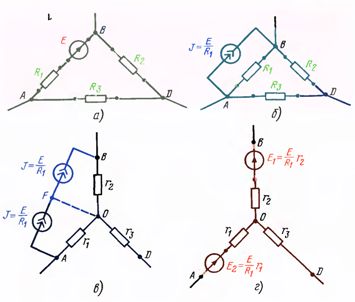
Если имеется три сопротивления, образующих три узла, то такие сопротивления составляют пассивный треугольник (рис. 1, а), а если имеется только один узел — то пассивную звезду (рис. 1,б). Слово "пассивный" означает, что внутри данной цепи отсутствуют какие-либо источники электрической энергии.
Обозначим сопротивления в цепи треугольника — большими (прописными) буквами (RAB, RBD, RDA), а в цепи звезды — малыми (ra, rb, rd).
Преобразование треугольника в звезду
Схему пассивного треугольника сопротивлений можно заменить эквивалентной схемой пассивной звезды, при этом все токи в ветвях, не подвергавшихся преобразованию (т. е. все, что на рис. 1, а и 1, б находится за пределами штриховой кривой), остаются без всяких изменений.
Например, если к узлам А, В, D в схеме треугольника притекали (или утекали) токи IА, IB, и ID, то и в схеме эквивалентной звезды к точкам А, В, D будут притекать (или утекать) те же самые токи IА, IB, и ID.
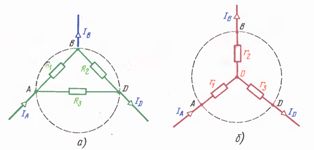
Рис. 1 Схемы соединения звездой и треугольником
Расчет сопротивлений в схеме звезды ra, rb, rd по известным сопротивлениям треугольника производятся по формулам
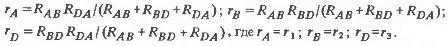
Данные выражения образуются по следующим правилам. Знаменатели у всех выражений одинаковые и представляют сумму сопротивлений треугольника, каждый числитель является произведением тех сопротивлений, которые в схеме треугольника примыкают к точке, к которой примыкают сопротивления звезды, определяемые в данном выражении.
Например, сопротивление гА в схеме звезды примыкает к точке А (см. рис. 1, б). Следовательно, в числителе следует написать произведение сопротивлений RAB и RDA, поскольку в схеме треугольника эти сопротивления примыкают к этой же точке А и т. д. Если известны сопротивления звезды ra, rb, rd, то можно рассчитать сопротивления эквивалентного треугольника RAB, RBD, RDA по формулам:
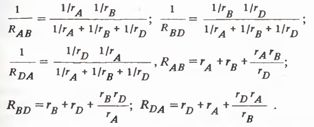
Из приведенных формул видно, что числители всех выражений одинаковые и представляют парные сочетания сопротивлений звезды, а в знаменателе записывается сопротивление, примыкающее к той точке звезды, к которой не примыкает искомое сопротивление треугольника.
Например, следует определить R1, т. е. сопротивление, примыкающее в схеме треугольника к точкам А и В, следовательно, в знаменателе должно быть сопротивление гэ = rd, поскольку это сопротивление в схеме звезды не примыкает ни к точке А, ни к точке В и т. д.
Преобразование треугольника сопротивлений с источником напряжения в эквивалентную звезду
Пусть имеется цепь (рис. 2, а).
Рис. 2. Преобразование треугольника сопротивлений с источником напряжения в эквивалентную звезду
Требуется преобразовать данный треугольник в звезду. Если бы в схеме не было источника Е, то преобразование можно было произвести с помощью формул преобразования пассивного треугольника в пассивную звезду. Однако данные формулы справедливы только для пассивных цепей, поэтому в цепях с источниками необходимо проделать ряд преобразований.
Заменим источник напряжения Е эквивалентным источником тока, цепь рис. 2, а приобретает вид рис. 2, б. В результате преобразования получился пассивный треугольник R1, R2, R3, который можно превратить в эквивалентную пассивную звезду, причем между точками АВ остается неизменнным источник J = E/Rt.
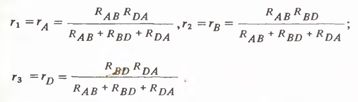
Расщепим источник J и соединим точку F с точкой 0 (на рис. 2, в показано штриховой линией). Теперь источники тока можно заменить эквивалентными источниками напряжения, при этом получается схема эквивалентной звезды с источниками напряжения (рис. 2, г).
