Поток и циркуляция векторного поля - это две важные характеристики векторных полей, которые используются в различных областях физики и математики. Они связаны с понятиями дивергенции и ротора векторного поля, а также с теоремами Гаусса-Остроградского и Стокса.
По материалам лекции Ричарда Фейнмана
При описании законов электричества с точки зрения векторных полей, перед нами открываются две математически важные характеристики векторного поля: поток и циркуляция. Хорошо бы разобраться, что это за математические понятия и в чем заключается их практический смысл.
На вторую часть вопроса легко ответить сразу, ведь понятия потока и циркуляции лежат в основе уравнений Максвелла, на которых, по сути, и держится вся современная электродинамика.
Так, например, закон электромагнитной индукции может быть сформулирован следующим образом: циркуляция напряженности электрического поля E по замкнутому контуру C равна скорости изменения потока магнитного поля B через площадь поверхности S, ограниченной данным контуром С.
Далее мы достаточно просто, на понятных примерах с жидкостью, опишем то, как математически определяются, из чего берутся и получаются данные характеристики поля.
Поток векторного поля
Для начала давайте изобразим вокруг исследуемой области пространства некую замкнутую поверхность совершенно произвольной формы. После того как мы эту поверхность изобразим, зададимся вопросом, вытекает ли через данную замкнутую поверхность исследуемый объект, который мы именуем полем? Чтобы понять о чем здесь идет речь, рассмотрим простой пример с жидкостью.
Допустим, мы исследуем поле скоростей некой жидкости. Для подобного примера имеет смысл поинтересоваться: вытекает ли в единицу времени через эту поверхность больше жидкости, нежели втекает внутрь объема ограниченного данной поверхностью? Другими словами, всегда ли скорость истечения направлена главным образом изнутри - наружу?
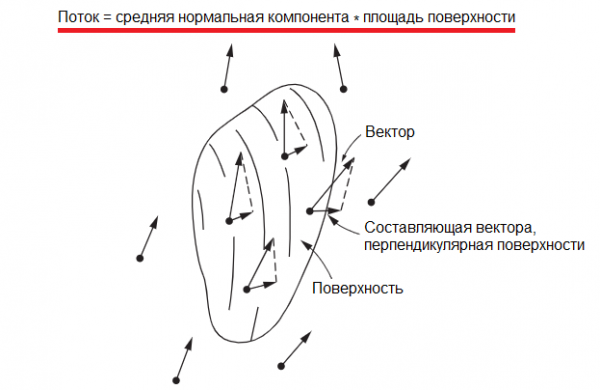
Словосочетанием «поток векторного поля» (а для нашего примера более точным будет выражение «поток скорости жидкости») договоримся именовать общее количество воображаемой жидкости, которая именно вытекает наружу через поверхность из рассматриваемого объема, ограниченного данной замкнутой поверхностью (для потока скорости жидкости — сколько жидкости вытекает из объема за единицу времени).
В результате, поток через элемент поверхности окажется равен произведению площади элемента поверхности на перпендикулярную составляющую скорости. Тогда общий (суммарный) поток через всю поверхность будет равен произведению средней нормальной составляющей скорости, которую будем отсчитывать изнутри наружу, на общую площадь поверхности.
Теперь вернемся к электрическому полю. Электрическое поле, конечно, нельзя считать скоростью течения какой-то жидкости, однако мы имеем право ввести математическое понятие потока, похожее на то, что мы описали выше как поток скорости жидкости.
Только в случае с электрическим полем, его поток может быть определен через среднюю нормальную компоненту напряженности электрического поля Е. Кроме того, поток электрического поля можно определить не обязательно через замкнутую поверхность, а через любую ограниченную поверхность, обладающую не равной нулю площадью S.
Циркуляция векторного поля
Всем хорошо известно, что поля можно для наглядности изображать в виде так называемых силовых линий, в каждой точке которых направление касательной совпадает с направлением напряженности поля.
Опять вернемся к аналогии с жидкостью и представим себе поле скоростей жидкости. Зададимся вопросом: циркулирует ли жидкость? То есть движется ли она преимущественно по направлению какого-то воображаемого замкнутого контура?
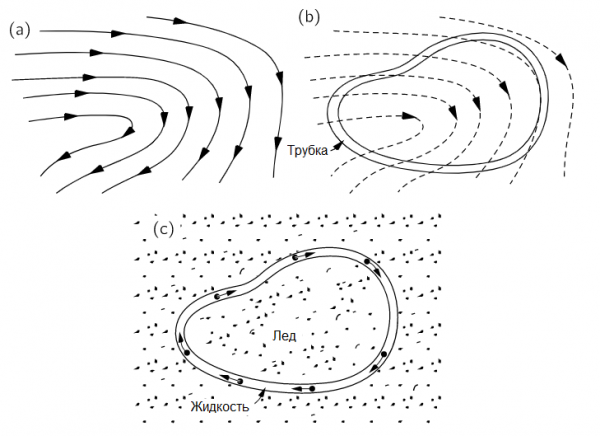
Для наглядности представим, что жидкость в неком большом сосуде как-то движется (рис a), и мы резко заморозили почти весь ее объем, но умудрились оставить не замороженным объем в форме ровной замкнутой трубки, в которой трение жидкости о стенки отсутствует (рис b).
За пределами этой трубки жидкость превратилась в лед, и поэтому больше не может двигаться, однако внутри трубки жидкость способна продолжить свое движение при условии что имеется преобладающий импульс, который гонит ее, например по часовой стрелке (рис c). Тогда произведение скорости жидкости в трубке на длину трубки мы и назовем циркуляцией скорости жидкости.
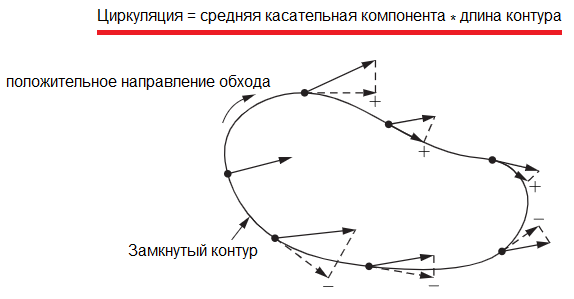
Подобным образом мы можем определить циркуляцию и для векторного поля, хотя, опять же, нельзя сказать, что поле является скоростью чего-то, тем не менее математическую характеристику «циркуляция» по контуру - определить можно.
Итак, циркуляция векторного поля по воображаемому замкнутому контуру может быть определена как произведение средней касательной компоненты вектора в направлении обхода контура - на длину контура.
Ричард Фейнман - известный американский физик, который сделал много открытий в области квантовой механики, квантовой электродинамики, супертекучести и других физических явлений. Он также был одним из участников Манхэттенского проекта, в котором разрабатывалась атомная бомба. За свои вклады в развитие квантовой электродинамики он получил Нобелевскую премию по физике в 1965 году вместе с Джулианом Швингером и Синъитиро Томонагой.
Фейнман также был известен своим нестандартным и оригинальным мышлением, своими популярными лекциями по физике, своими автобиографическими книгами, своими увлечениями музыкой, живописью и путешествиями. Он считался одним из самых влиятельных и вдохновляющих физиков XX века.