Сила, с которой электромагнит притягивает ферромагнитные материалы, зависит от магнитного потока Ф или, что то же самое, от индукции B и площади сечения электромагнита S.
Сила тяги электромагнита определяется по формуле
F=40550∙B^2∙S,
где F – сила тяги электромагнита, кГ (сила измеряется также в ньютонах, 1 кГ =9,81 Н, или 1 Н =0,102 кГ); B – индукция, Тл; S – площадь сечения электромагнита, м2.
Примеры
1. Электромагнит крана представляет собой магнитную цепь (рис. 1). Какую подъемную силу имеет подковообразный электромагнит крана, если магнитная индукция B=1 Тл, а площадь сечения каждого полюса электромагнита S=0,02 м2 (рис. 1, б)? Влиянием зазора между электромагнитом и якорем пренебречь.
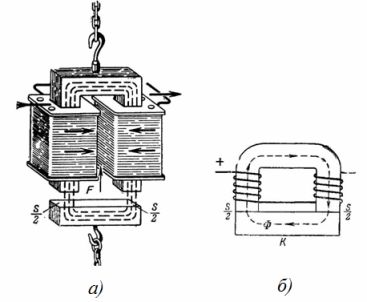
Рис. 1. Грузоподъемный электромагнит
F=40550∙B^2∙S; F=40550∙1^2∙2∙0,02=1622 кГ.
2. Круглый электромагнит из литой стали имеет размеры, указанные на рис. 2, а и б. Подъемная сила электромагнита равна 3 Т. Определить площадь сечения сердечника электромагнита, н. с. и число витков катушки при намагничивающем токе I=0,5 А.
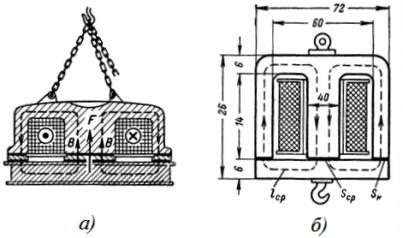
Рис. 2. Круглый электромагнит
Магнитный поток проходит по круглому внутреннему сердечнику и возвращается по цилиндрическому кожуху. Площади сечений сердечника Sс и кожуха Sк приблизительно одинаковы, поэтому и величины индукции в сердечнике и кожухе практически одинаковы:
Sс=(π∙40^2)/4=(3,14∙1600)/4=1256 см2 =0,1256 м2,
Sк=((72^2-60^2)∙π)/4=3,14/4∙(5184-3600)=1243,5 см2 =0,12435 м2;
S=Sс+Sк=0,24995 м2 ≈0,25 м2.
Необходимую индукцию в электромагните определим по формуле F=40550∙B^2∙S,
откуда B=√(F/(40550∙S))=√(3000/(40550∙0,25))=0,5475 Тл.
Напряженность при этой индукции находится по кривой намагничивания литой стали:
H=180 А/м.
Средняя длина силовой линии (рис. 2, б) lср=2∙(20+23)=86 см =0,86 м.
Намагничивающая сила I∙ω=H∙lср=180∙0,86=154,8 Ав; I=(I∙ω)/I=154,8/0,5=310 А.
В действительности н. с, т. е. ток и число витков, должна быть во много раз больше, так как между электромагнитом и якорем неизбежен воздушный зазор, который сильно увеличивает магнитное сопротивление магнитной цепи. Поэтому при расчете электромагнитов необходимо учитывать воздушный зазор.
3. Катушка электромагнита для крана имеет 1350 витков, по ней течет ток I=12 А. Размеры электромагнита указаны на рис. 3. Какой груз поднимает электромагнит на расстоянии 1 см от якоря и какой груз он может удержать после притяжения?
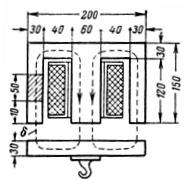
Рис. 3. Катушка электромагнита
Большая часть н. с. I∙ω тратится на проведение магнитного потока через воздушный зазор: I∙ω≈Hδ∙2∙δ.
Намагничивающая сила I∙ω=12∙1350=16200 А.
Так как H∙δ=8∙10^5∙B, то Hδ∙2∙δ=8∙10^5∙B∙0,02.
Отсюда 16200=8∙10^5∙B∙0,02, т. е. B=1,012 Тл.
Принимаем, что индукция B=1 Тл, так как часть н. с. I∙ω тратится на проведение магнитного потока в стали.
Проверим этот расчет по формуле I∙ω=Hδ∙2∙δ+Hс∙lс.
Средняя длина магнитной линии равна: lср=2∙(7+15)=44 см =0,44 м.
Напряженность Hс при B=1 Тл (10000 Гс) определим по кривой намагничивания:
Hс=260 А/м. I∙ω=0,8∙B∙2+2,6∙44=1,6∙10000+114,4=16114 Ав.
Намагничивающая сила I∙ω=16114 Ав, создающая индукцию B=1 Тл, практически равна заданной н. с. I∙ω=16200 Ав.
Общая площадь сечения сердечника и конуса равна: S=6∙5+2∙5∙3=0,006 м2.
Электромагнит притянет с расстояния 1 см груз весом F=40550∙B^2∙S=40550∙1^2∙0,006=243,3 кг.
Так как после притяжения якоря воздушный зазор практически исчезает, электромагнит может удержать гораздо больший груз. В этом случае вся н. с. I∙ω расходуется на проведение магнитного потока только в стали, поэтому I∙ω=Hс∙lс; 16200=Hс∙44; Hс=16200/44=368 А/см =36800 А/м.
При такой напряженности сталь практически насыщается и индукция в ней равна приблизительно 2 Тл. Электромагнит притягивает якорь с силой F=40550∙B^2∙S=40550∙4∙0,006=973 кГ.
4. Сигнальное (блинкерное) реле состоит из броневого электромагнита 1 с круглым сердечником и якоря клапанного типа 2, который после подачи тока в электромагнит притягивает и освобождает блинкер 3, открывающий сигнальную цифру (рис. 4).
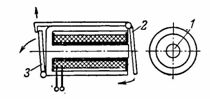
Рис. 4. Броневой электромагнит
Намагничивающая сила I∙ω=120 Ав, воздушный зазор δ=0,1 см, а общая площадь сечения электромагнита S=2 см2. Определить приблизительно силу притяжения реле.
Индукцию B определим путем последовательных приближений с помощью уравнения I∙ω=Hс∙lс+Hδ∙2∙δ.
Пусть н. с. Hс∙lс составляет 15% I∙ω, т. е. 18 Ав.
Тогда I∙ω-Hс∙lс=Hδ∙2∙δ; 120-18=Hδ∙0,2; Hδ=102/0,2=510 А/см =51000 А/м.
Отсюда находим индукцию B:
Hδ=8∙10^5 В; B=Hδ/(8∙10^5 )=51000/(8∙10^5 )=0,0637 Тл.
После подстановки значения B в формулу F=40550∙B^2∙S получим:
F=40550∙0,0637^2∙0,0002=0,0326 кГ.
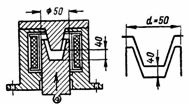
5. Тормозной электромагнит постоянного тока (рис. 5) имеет плунжерный якорь с конусным упором. Зазор между якорем и сердечником равен 4 см. Рабочий диаметр (сердечники круглой площади соприкосновения) d=50 мм. Якорь втягивается в катушку с силой 50 кГ. Длина средней силовой линии lср=40 см. Определить н. с. и ток катушки, если она имеет 3000 витков.
Рис. 5. Тормозной электромагнит постоянного тока
Площадь рабочего сечения электромагнита равна площади круга диаметром d=5 см:
S=(π∙d^2)/4=3,14/4∙25=19,6 см2.
Необходимую для создания силы F=50 кГ индукцию B найдем из уравнения F=40550∙B^2∙S,
откуда B=√(F/(40550∙S))=√(50/(40550∙0,00196))=0,795 Тл.
Намагничивающая сила I∙ω=Hс∙lс+Hδ∙δ.
Намагничивающую силу для стали Hс∙lс определим упрощенно, исходя из того, что она составляет 15% I∙ω:
I∙ω=0,15∙I∙ω+Hδ∙δ; 0,85∙I∙ω=Hδ∙δ; 0,85∙I∙ω=8∙10^5∙B∙δ; I∙ω=(8∙10^5∙0,795∙0,04)/0,85=30000 Ав.
Намагничивающий ток I=(I∙ω)/ω=30000/3000=10 А.