Емкость C есть способность конденсатора принять (накопить и удержать) количество электричества Q в ампер-секундах или заряд Q в кулонах. Если сообщить какому-либо телу, например шару, электрический заряд (количество электричества) Q, то электроскоп, включенный между этим телом и землей, покажет напряжение U (рис. 1). Это напряжение пропорционально заряду и зависит также от формы и размеров тела.
Зависимость между зарядом Q и напряжением U выражается формулой Q=C∙U.
Постоянная пропорциональности C называется емкостью тела. В случае, если тело имеет форму шара, емкость тела пропорциональна радиусу шара r.
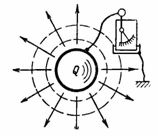
Рис. 1.
Единицей измерения емкости является фарада (Ф).
Емкостью 1 Ф обладает тело, когда при заряде 1 к между ним и землей получается напряжение 1 В. Фарада – очень большая единица измерения, а потому на практике используют более мелкие единицы: микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ).
Эти единицы связаны следующими соотношениями: 1 Ф =10^6 мкФ; 1 мкФ =10^6 пФ; 1 нФ =10^3 пФ.
Емкость шара радиусом 1 см равна 1,1 пФ.
Накапливать заряд может не только изолированное тело, но и специальное устройство, называемое конденсатором. Конденсатор состоит из двух или более пластин (обкладок), которые разделены диэлектриком (изоляцией).
На рис. 2 показана схема с источником постоянного тока, включенным на конденсатор. При включении на правой пластине конденсатора образуется положительный заряд +Q, а на левой пластине отрицательный заряд –Q. Во время заряда конденсатора по цепи протекает ток, который после окончания заряда прекращается; тогда напряжение на конденсаторе будет равно э. д. с. источника U. Заряд на обкладке конденсатора, напряжение и емкость связаны соотношением Q=C∙U. В диэлектрике конденсатора при этом образуется электростатическое поле.
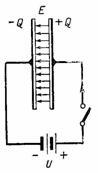
Рис. 2.
Емкость конденсатора с диэлектриком из воздуха можно подсчитать по формуле C=S/(4∙π∙d)∙1,11, пФ, где S – площадь одной обкладки, см2; d – расстояние между обкладками, см; C – емкость конденсатора, пФ.
Емкость конденсатора, состоящего из n пластин (рис. 3), равна: C=(n-1)∙ S/(4∙π∙d)∙1,11, пФ.
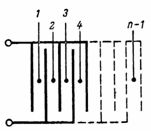
Рис. 3.
Если пространство между пластинами заполнить другим диэлектриком – например бумагой, емкость конденсатора увеличится в ε раз. При применении бумажной изоляции емкость увеличится в 3 раза, при слюдяной изоляции – в 5–8 раз, при стеклянной – в 7 раз и т. д. Величина ε называется диэлектрической проницаемостью диэлектрика.
Общая формула для определения емкости конденсатора с диэлектрической проницаемостью ε (эпсилон) имеет вид: C=ε∙S/(4∙π∙d)∙1,11, пФ.
Эта формула удобна для расчетов небольших переменных конденсаторов для радиоприемников. Эта же формула может быть представлена в виде: C=(ε_0∙ε∙S)/d, где ε_0 – диэлектрическая постоянная, или диэлектрическая проницаемость, вакуума (ε_0=8,859∙10^(-12) Ф/м); ε – диэлектрическая проницаемость диэлектрика.
В этой формуле размеры подставляются в метрах, а емкость получается в фарадах.
Примеры
1. Какую емкость имеет планета Земля, радиус которой r=6378 км?
Так как емкость шара радиусом 1 см равна 1,11 пФ, то емкость Земли равна: C=637,8∙10^6∙1,11=707,95∙10^6 пФ =708 мкФ. (Емкость шара, равного по величине нашей планете, сравнительно невелика. Такую емкость имеют небольшие по размерам электролитические конденсаторы).
2. Определить емкость конденсатора, состоящего из двух пластин, каждая из которых имеет площадь S=120 см2.
Пластины разделены слоем воздуха толщиной d=0,5 см, C=S/(4∙π∙d)∙1,11= (120∙1,11)/(4∙π∙0,5)=21,20 пФ.
3. Определить емкость конденсатора с данными, указанными в предыдущем примере, если пространство между пластинами будет заполнено парафинированной бумагой с диэлектрической проницаемостью ε=4, стеклом (ε=7), электротехническим картоном (ε=2), слюдой (ε=8).
Конденсатор с парафинированной бумагой имеет емкость C=ε∙(S∙1,11)/(4∙π∙d)=4∙21,2=84,8 пФ.
Емкость конденсатора со стеклом C=7∙21,2=148,4 пФ.
Емкость конденсатора с картоном C=2∙21,2=42,3 пФ.
Емкость конденсатора со слюдой C=8∙21,2=169,6 пФ.
4. Какова емкость воздушного поворотного конденсатора для радиоприемника, состоящего из 20 пластин площадью 20 см2, если расстояние между пластинами 0,06 см (рис. 149)?
C=(n-1)∙(S∙1,11)/(4∙π∙d)=(20-1)∙(20∙1,11)/(4∙π∙0,06)=559,44 пФ.
Конденсатор, изображенный на рис. 3, состоит из отдельных простейших конденсаторов с двумя обкладками, число которых равно n-1.
5. Бумажный конденсатор емкостью C=2 мкФ состоит из двух полос станиоля C и двух полос диэлектрика из парафинированной бумаги Б с диэлектрической проницаемостью ε=6. Толщина парафинированной бумаги d=0,1 мм. Сложенные полосы сворачиваются в рулон, от станиолевых обкладок делаются выводы. Определить длину станиолевой полосы конденсатора, если ее ширина 4 см (рис. 4).
Рис. 4.
Сначала определим площадь S одной полосы по формуле C=ε∙S/(4∙π∙d)∙1,11, откуда S=(C∙4∙π∙d)/(ε∙1,11)=(2∙4∙π∙0,01∙10^6)/(6∙1,11); S=2000000/(6∙1,11)∙4∙π∙0,01=37680 см2.
Длина каждой полосы l=37680/4=9420 см =94,2 м.