
Допустимая удельная поверхностная мощность PF=P⁄F,
где Р – мощность проволочного нагревателя, Вт;
F=π∙d∙l – площадь поверхности нагревателя, м2; l – длина провода, м.
Согласно первому методу
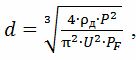
где ρд – удельное электрическое сопротивление материала провода при действительной температуре, Ом•м; U – напряжение проволочного нагревателя, В; PF – допустимые значения удельной поверхностной мощности для различных нагревателей:
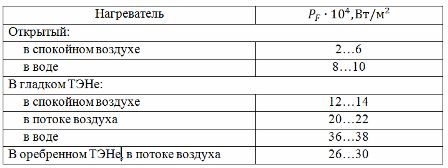
Во втором методе используют таблицу токовых нагрузок (см. таблицу 1), составленную по экспериментальным данным. Для того чтобы воспользоваться указанной таблицей, необходимо определить расчетную температуру нагрева Tр, связанную с действительной (или допустимой) температурой провода Tд соотношением:
Tр=Kм∙Kс∙Tд,
где Kм – коэффициент монтажа, учитывающий ухудшение условий охлаждения нагревателя из-за его конструктивного исполнения; Kс – коэффициент среды, учитывающий улучшение условий охлаждения нагревателя по сравнению с неподвижной воздушной средой.
Для нагревательного элемента из провода, свитого в спираль, Kм=0,8…0,9; то же, с керамическим основанием Kм=0,6…0,7; для провода нагревательных плиток и некоторых ТЭНов Kм=0,5…0,6; для провода электронагревателей пола, почвы и ТЭНов Kм=0,3…0,4. Меньшее значение Kм соответствует нагревателю меньшего диаметра, большее – большего диаметра.
При работе в условиях, отличающихся от свободной конвекции, для нагревательных элементов в воздушном потоке принимают Kс=1,3…2,0; для элементов в неподвижной воде Kс=2,5; в потоке воды – Kс=3,0…3,5.
Если заданы напряжение Uф и мощность Pф будущего (проектируемого) нагревателя, то его ток (на одну фазу)
Iф=Pф⁄Uф
По расчетному значению тока нагревателя для требуемой расчетной температуры его нагрева по таблице 1 находят необходимый диаметр нихромового провода d и рассчитывают необходимую длину провода, м, для изготовления нагревателя:
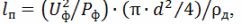
где d – выбранный диаметр провода, м; ρд – удельное электрическое сопротивление провода при действительной температуре нагрева, Ом•м,
ρд=ρ20∙[1+αр∙(Tд-20)],
где αр – температурный коэффициент сопротивления, 1/оС.
Для того чтобы определить параметры спирали из нихрома, принимают средний диаметр витков D=(6…10)∙d, шаг спирали h=(2…4)∙d,
число витков
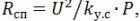
длину спирали lсп=h∙n.
« Подписывайтесь на наши каналы в Telegram: Школа для электрика и Электрика, электромонтажные работы
При расчете ТЭНов следует помнить, что сопротивление провода спирали после опрессовки ТЭНа
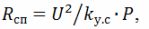
где k(у.с) – коэффициент, учитывающий уменьшение сопротивления спирали; по опытным данным k(у.с)=1,25. Следует также учитывать, что удельная поверхностная мощность провода спирали больше в 3,5...5 раз удельной поверхностной мощности на трубке ТЭНа.
В практических расчетах ТЭНа сначала определяют температуру на его поверхности Tп=Tо+P∙Rт1,
где Tо – температура окружающей среды, °С; P – мощность ТЭНа, Вт; Rт1 – термическое сопротивление на границе трубка – среда, оС/Вт.
Затем определяют температуру спирали: Tсп=Tо+P∙(Rт1+Rт2+Rт3 ),
где Rт2 – термическое сопротивление стенки трубки, оС/Вт; Rт3 – термическое сопротивление наполнителя, оС/Вт; Rт1=1⁄(α∙F), где α – коэффициент теплоотдачи, Вт/(м^2•оС); F – площадь поверхности нагревателя, м2; Rт2=δ⁄(λ∙F), где δ – толщина стенки, м; λ – теплопроводность стенки, Вт/(м•оС).
Подробнее про устройство ТЭНов смотрите здесь: ТЭНы. Устройство, выбор, эксплуатация, подключение ТЭНов
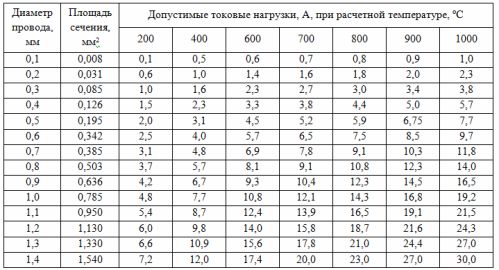
Таблица 1. Таблица токовых нагрузок
Пример 1. Рассчитать электрический нагреватель в виде проволочной спирали по допустимой удельной поверхностной мощности PF.
Условие. Мощность нагревателя P=3,5 кВт; напряжение питания U=220 В; материал провода – нихром Х20Н80 (сплав из 20 % хрома и 80 % никеля), поэтому удельное электрическое сопротивление провода ρ20=1,1∙10^(-6) Ом•м; температурный коэффициент сопротивления αр=16∙10^(-6) 1/оС; спираль открытая, находится в металлической пресс-форме, рабочая температура спирали Tсп=400 оС, PF=12∙10^4 Вт/м2. Определить d, lп, D, h, n, lсп.
Решение. Сопротивление проволочной спирали: R=U^2⁄P=220^2⁄3500=13,8 Ом.
Удельное электрическое сопротивление при Tсп=400 оС
ρ400=1,1∙10^(-6)∙[1+16∙10^(-6)∙(400-20) ]=1,11∙10^(-6) Ом•м.
Находим диаметр провода:

Из выражения R=(ρ∙l)⁄S получаем l⁄d^2 =(π∙R)⁄(4∙ρ), откуда длина провода
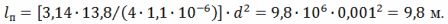
Средний диаметр витка спирали D=10∙d=10∙0,001=0,01 м=10 мм. Шаг спирали h=3∙d=3∙1=3 мм.
Число витков спирали
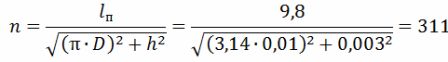
Длина спирали lсп=h∙n=0,003∙311=0,933 м=93,3 см.
Пример 2. Конструктивно рассчитать проволочный нагреватель сопротивления при определении диаметра провода d с помощью таблицы токовых нагрузок (см. табл. 1).
Условие. Мощность проволочного нагревателя P=3146 Вт; напряжение питания U=220 В; материал провода – нихром Х20Н80 ρ20=1,1∙10^(-6) Ом•м; αр=16∙10^(-6) 1/℃; спираль открытая, расположенная в потоке воздуха (Kм=0,85, Kс=2,0); допустимая рабочая температура провода Tд=470 оС.
Определить диаметр d и длину провода lп.
Решение.
Tр=Kм∙Kс∙Tд=0,85∙2∙470 оС=800 оС.
Ток проектируемого нагревателя I=P⁄U=3146⁄220=14,3 А.
По таблице токовых нагрузок (см. табл. 1) при Tр=800 оС и I=14,3 А находим диаметр и сечение провода d=1,0 мм и S=0,785 мм2.
Длина провода lп=(R∙S)⁄ρ800,
где R=U^2⁄P=220^2⁄3146=15,3 Ом, ρ800=1,1∙10^(-6)∙[1+16∙10^(-6)∙(800-20)]=1,11∙10^(-6) Ом•м, lп=15,3∙0,785∙10^(-6)⁄(1,11∙10^(-6) )=10,9 м.
Далее при необходимости аналогично первому примеру могут быть определены D, h, n, lсп.
Пример 3. Определить допустимое напряжение на трубчатом электрическом нагревателе (ТЭНе).
Условие. Спираль ТЭНа выполнена из нихромовой проволоки диаметром d=0,28 мм и длиной l=4,7 м. ТЭН находится в спокойном воздухе, имеющем температуру 20 оС. Характеристика нихрома: ρ20=1,1∙10^(-6) Ом•м; αр=16∙10^(-6) 1/°С. Длина активной части оболочки ТЭНа Lа=40 см.
ТЭН гладкий, наружный диаметр dоб=16 мм. Коэффициент теплоотдачи α=40 Вт/(м^2∙°С). Термические сопротивления: наполнителя Rт3=0,3 оС/Вт, стенки оболочки Rт2=0,002 оС/Вт.
Определить, какое максимальное напряжение можно приложить к ТЭНу, чтобы температура его спирали Tсп не превышала 1000 ℃.
Решение. Температура спирали ТЭНа
Tсп=Tо+P∙(Rт1+Rт2+Rт3),
где Tо – температура окружающего воздуха; P – мощность ТЭНа, Вт; Rт1 – контактное термическое сопротивление на границе трубка – среда.
Мощность ТЭНа P=U^2⁄R,
где R – сопротивление спирали нагревателя. Следовательно, можем записать Tсп-Tо=U^2/R∙(Rт1+Rт2+Rт3), откуда напряжение на ТЭНе
U=√((R∙(Tсп-Tо ))/(Rт1+Rт2+Rт3)).
Найдем R=ρ∙(4∙l)⁄(π∙d^2),
где ρ1000=ρ20∙[1+αр∙(T-20)]=1,1∙10^(-6)∙[1+16∙10^(-6)∙(1000-20)]=1,12∙10^(-6) Ом•м.
Тогда R=1,12∙10^(-6)∙(4∙4,7) ⁄ (3,14∙(0,28∙10^(-3) )^2)=85,5 Ом.
Контактное термическое сопротивление Rт1=1⁄(α∙F),
где F – площадь активной части оболочки ТЭНа; F=π∙dоб∙Lа=3,14∙0,016∙0,4=0,02 м2.
Находим Rт1=1⁄(40∙0,02=1,25) оС/Вт.
Определяем напряжение на ТЭНе U=√((85,5∙(1000-20)) / (1,25+0,002+0,3))=232,4 В.
Если номинальное напряжение, указанное на ТЭНе, равно 220 В, то перенапряжение при Tсп=1000 оС составит 5,6%∙Uн.


