Взаимодействие параллельных проводников с током (параллельных токов) - это явление, при котором два проводника, по которым течет электрический ток, притягиваются или отталкиваются друг от друга в зависимости от направления тока. Это взаимодействие объясняется действием магнитного поля, создаваемого токами в проводниках. Это явление называется законом Ампера.
Знание того как взаимодействуют параллельные проводники с током имеет важное значение для понимания и применения магнитных явлений в электротехнике, электронике, связи, медицине и других областях. Например, взаимодействие параллельных проводников с током используется для создания электромагнитов, генераторов, трансформаторов, электродвигателей, динамиков, микрофонов и т.д.
Определить в некоторой точке пространства вектор индукции магнитного поля B, порождаемого постоянным электрическим током I, можно с помощью Закона Био-Савара. Это делается путем суммирования всех вкладов в магнитное поле от отдельных элементов тока.
Жан Батист Био и Феликс Савар - французские физики, которые совместно открыли и сформулировали закон, связывающий электрический ток и магнитное поле. Закон Био-Савара позволяет рассчитывать магнитное поле в любой точке пространства, если известно распределение токов в проводниках.
Этот закон был получен на основе экспериментальных данных в 1820 году, вскоре после открытия Эрстеда о влиянии тока на магнитную стрелку. Закон Био-Савара является одним из основных законов магнитостатики и электромагнетизма.
Магнитное поле элемента тока dI, в точке, заданной вектором r, по Закону Био-Савара находится так (в системе СИ):
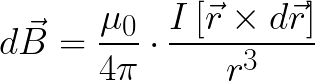
Одна из типичных задач состоит в том, чтобы далее определить силу взаимодействия двух параллельных токов. Ведь токи, как известно, порождают собственные магнитные поля, а ток, находящийся в магнитном поле (другого тока) испытывает на себе действие силы Ампера.
Французский физик Андре-Мари Ампер считается одним из основателей электродинамики. Его именем названа единица измерения силы электрического тока в Международной системе единиц.
Сила Ампера - это сила, действующая на проводник с током со стороны магнитного поля. Она зависит от индукции магнитного поля, от направления этой индукции, от тока в проводнике и длины проводника.
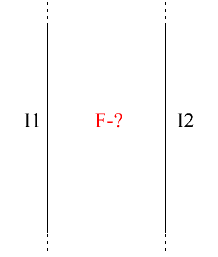
Под действием силы Ампера, противоположно направленные токи взаимно отталкиваются, а токи направленные в одну сторону - взаимно притягиваются.
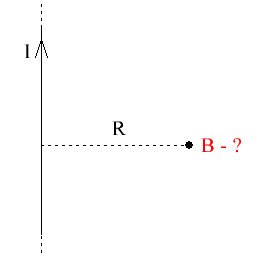
Прежде всего для прямого тока I нам необходимо найти магнитное поле B на некотором расстоянии R от него.
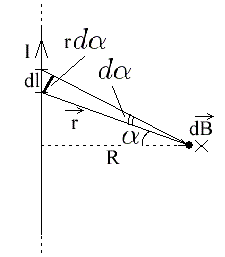
Для этого вводится элемент длины тока dl (по направлению тока), и рассматривается вклад от тока в месте расположения данного элемента длины - в общую индукцию магнитного поля применительно к выбранной точке пространства.
Сначала будем записывать выражения в системе СГС, то есть появится коэффициент 1/с, а в конце приведем запись в системе СИ, где появится магнитная постоянная.
По правилу нахождения векторного произведения, вектор dB - результат векторного произведения dl на r для любого элемента dl, в каком бы месте рассматриваемого проводника он не находился, всегда будет направлен за плоскость рисунка. Результат будет равен:
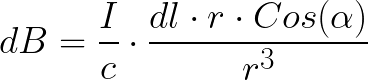
Произведение косинуса на dl можно выразить через r и угол:
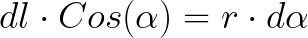
Значит выражение для dB примет вид:
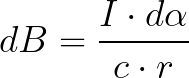
Далее выразим r через R и косинус угла:
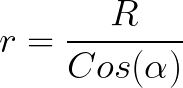
И выражение для dB примет вид:
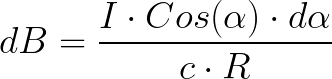
Далее необходимо это выражение проинтегрировать в пределах от -пи/2 до +пи/2, и в результате получим для B в точке на расстоянии R от тока следующее выражение:
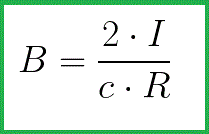
Можно сказать, что вектор B найденной величины, для выбранной окружности радиуса R, через центр которой перпендикулярно проходит данный ток I, всегда будет направлен по касательной к данной окружности, какую бы точку окружности мы ни выбрали. Здесь присутствует осевая симметрия, так что вектор B в любой точке окружности получается одной и той же длины.
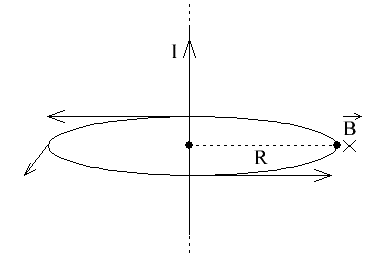
Теперь рассмотрим параллельные постоянные токи и решим задачу нахождения сил их взаимодействия. Допустим, что параллельные токи направлены в одну и ту же сторону.
Изобразим магнитную силовую линию в форме окружности радиуса R (о которой речь шла выше). И пусть второй проводник расположен параллельно первому в какой-то точке данной силовой линии, то есть в месте с индукцией, значение которой (в зависимости от R) мы только что научились находить.
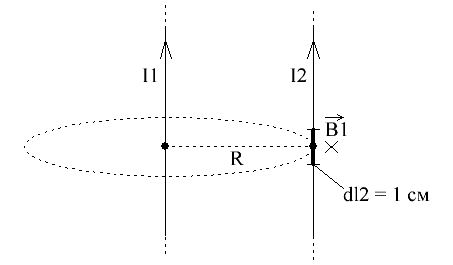
Магнитное поле в этом месте направлено за плоскость рисунка, и оно действует на ток I2. Выделим элемент длины тока l2, равный одному сантиметру (единица длины в системе СГС). Далее рассмотрим силы, действующие на него. Будем использовать Закон Ампера. Индукцию в месте расположения элемента длины dl2 тока I2 мы нашли выше, она равна:
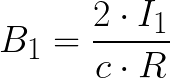
Следовательно сила, действующая со стороны всего тока I1 на единицу длины тока I2 будет равна:
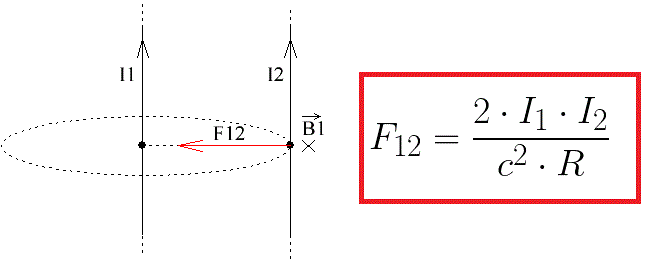
Это и есть сила взаимодействия двух параллельных токов. Поскольку токи однонаправленные и они притягиваются, то сила F12 со стороны тока I1 направлена так, что она тянет ток I2 в сторону тока I1. Со стороны же тока I2 на единицу длины тока I1 действует сила F21 равной величины, но направленная в сторону противоположную силе F12, в соответствии с третьим законом Ньютона.
В системе СИ, сила взаимодействия двух постоянных параллельных токов находится по следующей формуле, где коэффициент пропорциональности включает в себя магнитную постоянную:
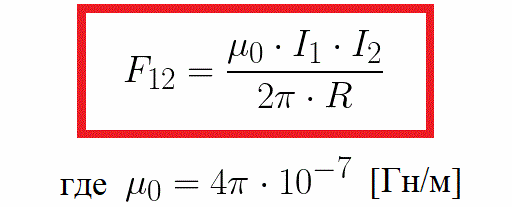
Эта формула была получена Ампером на основе экспериментальных данных.
Она показывает, что сила взаимодействия прямо пропорциональна силам токов и длине проводников, а обратно пропорциональна расстоянию между ними.
Также из формулы следует, что если токи текут в одном направлении, то сила взаимодействия положительна, то есть проводники притягиваются, а если токи текут в противоположных направлениях, то сила взаимодействия отрицательна, то есть проводники отталкиваются. Это соответствует наблюдаемому явлению взаимодействия параллельных токов.
Андрей Повный



