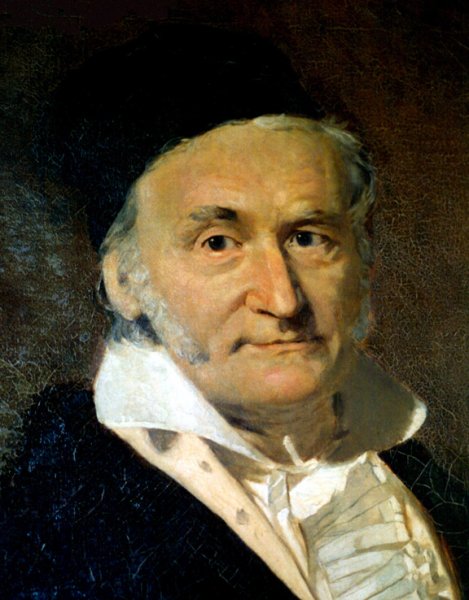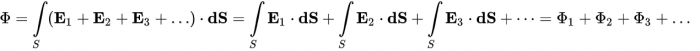Теорема Гаусса (закон Гаусса) считается одим из основных законов электродинамики и входит в систему уравнений Максвелла.
В ряде случаев любую электростатическую задачу можно было бы начинать решать с нахождения в каждой интересующей нас точке пространства электрических сил и соответствующих напряженностей, исходя из закона Кулона. Давайте, однако, посмотрим на картину электрических зарядов несколько шире.
Для начала изобразим с помощью силовых линий геометрическую картину электрического поля, создаваемого положительным точечным зарядом в точке О. Силовые линии будут исходить из положительного заряда. В случае отрицательного заряда, силовые линии будут заканчиваться на нем.
Практически любое электростатическое поле представляет собой результирующую картину, образованную полями отдельных зарядов, - говорит нам принцип суперпозиции полей.
Но можно ли здесь обнаружить некую более обобщенную закономерность, чтобы не начинать все время с закона Кулона? Можно! Одна из теорем, позволяющих облегчить решение многих задач, — теорема Гаусса.
Карл Фридрих Гаусс — великий немецкий ученый первой половины 19 века, сделавший очень много как для математики, так и для физики.
Для начала представим себе, что в некоторой области пространства есть какое-то электростатическое поле. Выберем в этой области некоторую незамкнутую поверхность и рассмотрим на данной поверхности произвольную точку. В этой точке электрическое поле может быть описано с помощью вектора E – вектора напряженности электрического поля.
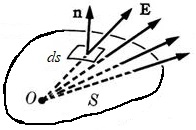
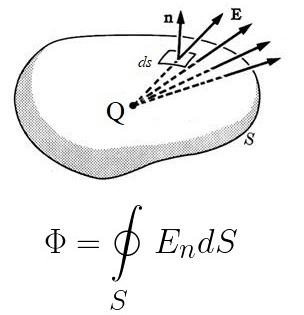
Выберем на поверхности, в окрестности рассматриваемой точки, маленькую площадку dS, и изобразим наружную нормаль n к ней. Спроектируем вектор E на направление нормали и умножим значение этой проекции на элемент площади ds.
Полученное произведение будет представлять собой элементарный поток dФ вектора E через площадку ds. Пусть вся площадь незамкнутой поверхности будет равна S. Тогда полный поток поля E через всю эту поверхность можно будет найти с помощью интегрирования. Здесь и далее будем использовать систему СГС.
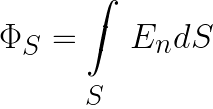
Выберем теперь некоторую замкнутую поверхность S и найдем поток вектора E применительно к ней.
Изобразим здесь внешнюю нормаль n к элементарной площадке dS. Найдем элементарный поток dФ и проинтегрируем по всей замкнутой поверхности. Получится поток вектора E через замкнутую поверхность S.
Теорема Гаусса утверждает, что если в пространстве, в котором имеет место электростатическое поле, выбрать произвольную замкнутую поверхность, то поток вектора E через эту поверхность всегда будет пропорционален заряду, попавшему в область, ограниченную данной поверхностью. Далее это будет проиллюстрировано.
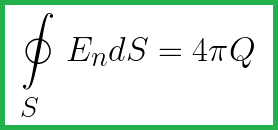
Q – заряд внутри области пространства, ограниченной данной замкнутой поверхностью.
Важно понимать, что заряд (источник электрического поля) - это не обязательно один единственный точечный заряд или единственное заряженное тело. Рассматриваемое электрическое поле может быть создано и несколькими заряженными телами. Но если в область, ограниченную рассматриваемой поверхностью, попадает лишь одно из этих тел, то в расчет потока принимается лишь оно одно.
«
Подписывайтесь на наши каналы в Telegram:
Школа для электрика и Электрика, электромонтажные работы
Кстати, понятие потока пришло в электростатику по аналогии, из теории течения идеальной жидкости. Практически, скорость течения жидкости, умноженная на площадь, даст нам представление об объеме жидкости, вытекающей наружу за единицу времени.
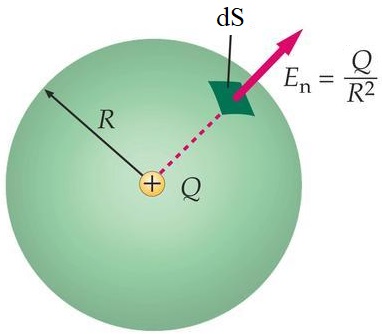
Что если поверхность сферическая? Рассмотрим точечный заряд Q, окружим его сферой радиуса R, имеющей площадь S. Исходя из закона Кулона, найдем напряженность электрического поля в любой точке поверхности данной сферы.
Из соображений симметрии, вектор напряженности везде будет направлен по нормали, по радиусу. Следовательно для нахождения потока, достаточно умножить выражение для напряженности поля на площадь сферы. Вот и доказательство теоремы Гаусса для частного случая — для поверхности в форме сферы.
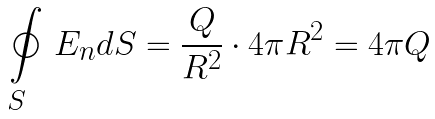
Но что, если замкнутая поверхность не сферическая, а произвольной формы? Давайте разбираться. Рассмотрим в области, ограниченной данной поверхностью, точечный заряд q.
Выберем кусочек поверхности dS. Построим элементарный телесный угол, который вырежет на поверхности такой кусочек. Изобразим внешнюю нормаль к этому кусочку поверхности, а также вектор E.
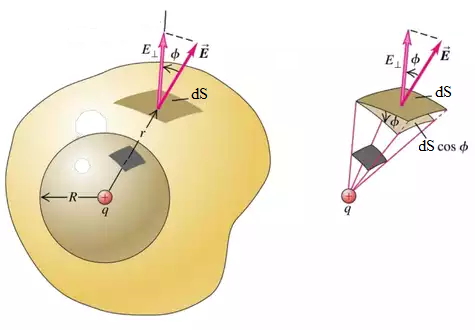
Поток через кусочек поверхности будет равен:
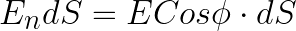
Но данное выражение — это есть такой же поток вектора E, как если бы телесный угол вырезал площадку dS не на произвольной, а на сферической поверхности! Поэтому нет разницы, сферическая поверхность или не сферическая, главное — она должна быть замкнутой. Для нахождения потока имеет значение лишь площадь поверхности.
И даже если изменится площадь, все равно поток останется пропорциональным лишь заряду, находящемуся в области, ограниченной данной поверхностью.
Потому что, если рассмотреть сферу меньшего радиуса, то при одном и том же телесном угле, площади вырезаемых площадок будут относиться как квадраты радиусов, а напряженности поля на этих площадках — всюду будут обратно пропорциональны квадрату радиусов (это следует из закона Кулона). Поэтому и произведения напряженностей и площадей будут одинаковыми.
А если поверхность не охватывает исследуемый заряд, что тогда? Тогда, если изобразить телесный угол, то он выделит на поверхности две площадки.
Вектор напряженности электрического поля в одном месте поверхности будет направлен в одну сторону с внешней нормалью, а в другом месте — в сторону противоположную по отношению ко внешней нормали.
В результате два равных по модулю потока (один положительный, другой — отрицательный) через одну и ту же поверхность в сумме дадут ноль. Потока (наружу) из области, охватываемой поверхностью, существовать не будет.
Но как быть, если существует сложное распределение зарядов внутри поверхности, а не один точечный заряд? Очень просто!
Согласно принципу суперпозиции, любое распределение зарядов даст сумму электрических напряженностей. И поток суммы будет равен сумме потоков, исходя из принципа суперпозиции полей. То есть достаточно просто просуммировать интегралы от поля каждого заряда по поверхности.
Таким образом, для произвольного распределения зарядов теорема Гаусса - тоже верна.
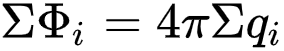
Расчет электростатических полей, основанный на принципе суперпозиции, достаточно сложен, хотя с его помощью можно рассчитать поле любой системы зарядов. В ряде случаев значительно более простым оказывается метод, основанный на применении теоремы Гаусса. Особенно удобен этот метод для симметричного расположения зарядов.
Теорема Гаусса верна для любых полей, для которых одновременно верны принцип суперпозиции и закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, чем закон Кулона.
Смотрите также: Проводники в электрическом поле
Андрей Повный