В физике линия в пространстве, начинающаяся из одной точки в другую, называется вектором, то есть она имеет направление и значение. Функция векторов в физике — это выражение так называемых векторных величин.
Векторные величины — это такие величины, которые, выражены в пространстве с помощью векторов. Это отличает их от скалярных величин, для которых требуется только одно число и одна единица измерения.
Смотрите также - Физические величины и параметры, скалярные и векторные величины, скалярные и векторные поля
Для электрических цепей переменного тока в установившемся режиме можно использовать для исследования векторный метод, избегая решения дифференциальных уравнений. Векторное представление синусоидального сигнала, широко используемое в электротехнике.
Векторные диаграммы — метод графического расчета напряжений и токов в цепях переменного тока, в которых переменные напряжения и токи символически (условно) изображаются с помощью векторов.
В основе метода лежит тот факт, что всякую величину, меняющуюся по синусоидальному закону (смотрите - синусоидальные колебания), можно определить как проекцию на какое-то выбранное направление вектора, вращающегося вокруг своей начальной точки с угловой скоростью, равной угловой частоте колебаний изображаемой переменной величины.
Поэтому всякое переменное напряжение (или переменный ток), меняющееся по синусоидальному закону, можно изображать с помощью такого вектора, вращающегося с угловой скоростью, равной угловой частоте изображаемого тока, причем длина вектора в определенном масштабе изображает амплитуду напряжения, а угол — начальную фазу этого напряжения.
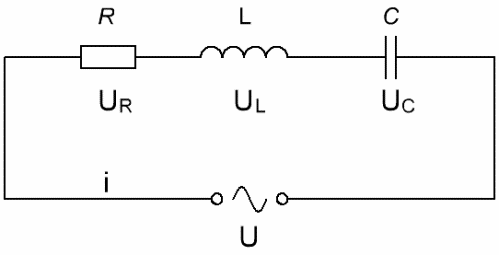
Если рассмотреть электрическую цепь, состоящую из последовательно соединенных источника переменного тока, резистора, индуктивности и конденсатора, где U – мгновенное значение переменного напряжения, а i – это ток в текущий момент времени, причем U изменяется по синусоидальному (косинусоидальному) закону, то для тока можно записать:
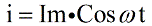
Согласно закону сохранения заряда, в любой момент времени ток в цепи имеет одно и то же значение. Следовательно на каждом элементе будет падать напряжение: UR – на активном сопротивлении, UC – на конденсаторе, и UL – на индуктивности. Согласно второму правилу Кирхгофа, напряжение источника будет равно сумме падений напряжений на элементах цепи, и мы имеем право записать:
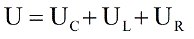
Заметим, что согласно закону Ома: I = U/R, и тогда U = I*R. Для активного сопротивления значение R определяется исключительно свойствами проводника, оно не зависит ни от тока, ни от момента времени, следовательно ток совпадает по фазе с напряжением, и можно записать:
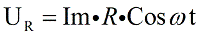
А вот конденсатор в цепи переменного тока обладает реактивным емкостным сопротивлением, и напряжение на конденсаторе все время отстает по фазе от тока на Пи/2, значит пишем:
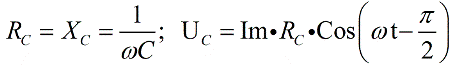
Катушка, обладающая индуктивностью, в цепи переменного тока выступает реактивным индуктивным сопротивлением, и напряжение на катушке в любой момент времени опережает по фазе ток на Пи/2, следовательно, для катушки запишем:
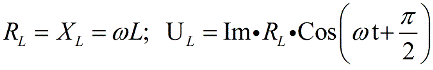
Можно записать теперь сумму падений напряжений, но в общем виде для приложенного к цепи напряжения можно записать:
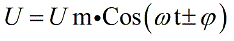
Видно, что здесь имеет место некий сдвиг фаз, связанный с реактивной составляющей общего сопротивления цепи при протекании по ней переменного тока.
Поскольку в цепях переменного тока и ток и напряжение изменяются по закону косинуса, причем мгновенные значения отличаются между собой лишь фазой, то физики придумали в математических расчетах рассматривать токи и напряжения в цепях переменного тока как векторы, поскольку тригонометрические функции можно описать через векторы. Итак, запишем напряжения в виде векторов:
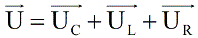
Используя метод векторных диаграмм, можно вывести, например, закон Ома для данной последовательной цепи в условиях протекания по ней переменного тока.
Согласно закону сохранения электрического заряда, в любой момент времени ток во всех частях данной цепи одинаков, так отложим же векторы токов, построим векторную диаграмму токов:
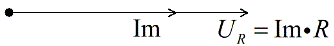
Пусть в направлении оси Х будет отложен ток Im – амплитудное значение тока в цепи. Напряжение на активном сопротивлении совпадает по фазе с током, значит эти векторы будут сонаправленными, отложим их из одной точки.
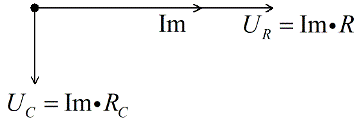
Напряжение на конденсаторе отстает на Пи/2 от тока, следовательно откладываем его под прямым углом вниз, перпендикулярно вектору напряжения на активном сопротивлении.
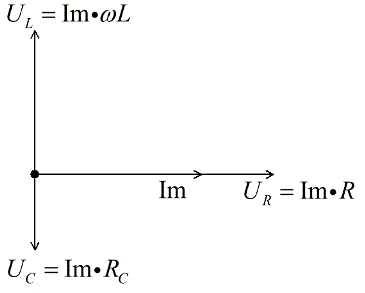
Напряжение на катушке опережает на Пи/2 ток, следовательно, откладываем его под прямым углом вверх, перпендикулярно вектору напряжения на активном сопротивлении. Допустим, что для нашего примера UL>UC.
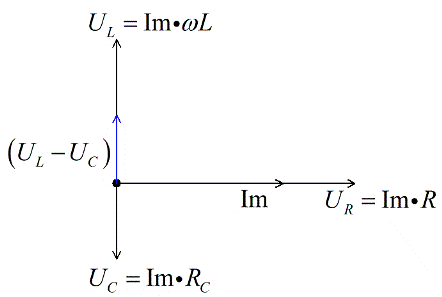
Поскольку мы имеем дело с векторным уравнением, сложим векторы напряжений на реактивных элементах, и получим разницу. Она будет для нашего примера (мы приняли что UL>UC) направлена вверх.
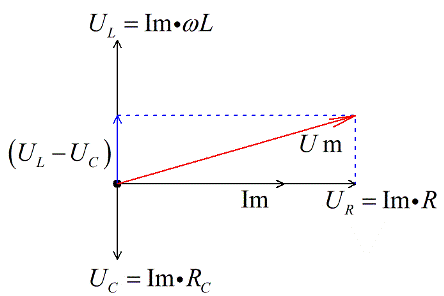
Прибавим теперь вектор напряжения на активном сопротивлении, и получим, по правилу векторного сложения, вектор суммарного напряжения. Так как брали максимальные значения, то и получим вектор амплитудного значения общего напряжения.
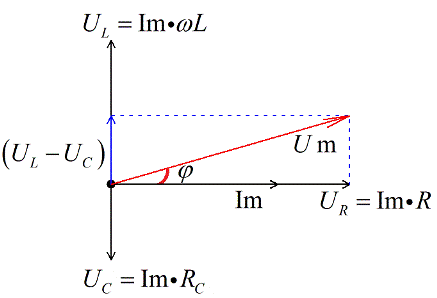
Так как ток менялся по закону косинуса, то напряжение тоже меняется по закону косинуса, но со сдвигом фаз. Между током и напряжением есть постоянный сдвиг фаз.
Запишем закон Ома для общего сопротивления Z (импеданса):
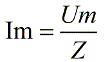
Из векторных изображений по Теореме Пифагора можем записать:
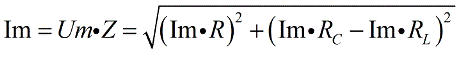
После элементарных преобразований получим выражение для полного сопротивления Z цепи переменного тока, состоящей из R, C и L:
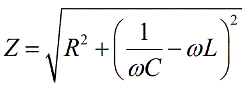
Тогда получим выражение для закона Ома для цепи переменного тока:
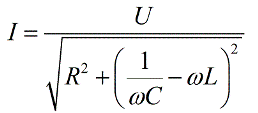
Заметим, что наибольшее значение тока получатся в цепи при резонансе в условиях, когда:
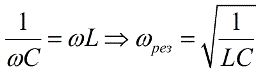
Косинус фи из наших геометрических построений получается:
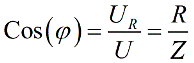
Андрей Повный