Как известно, для решения некоторых типичных задач электротехники применяют комплексные числа. Но для чего их используют и почему это делают именно так? В этом мы и постараемся разобраться по ходу данной статьи. Дело в том, что комплексный метод, или метод комплексных амплитуд, удобен при расчетах сложных цепей переменного тока. И для начала вспомним немного математических основ:

Как видите, комплексное число z включает в себя мнимую и действительную части, которые между собой различаются и обозначаются в тексте по-разному. Само же комплексное число z может быть записано в алгебраической, тригонометрической или показательной форме:

Комплексные числа появились в результате решения уравнений, в которых под корнем получалось отрицательное число. Такие уравнения не имели решений в множестве действительных чисел, поэтому было введено понятие мнимой единицы i, которая является корнем из -1. С помощью комплексных чисел можно решать любые алгебраические уравнения, а также изучать различные функции и преобразования комплексного аргумента.
Исторические предпосылки
Считается, что представление о мнимых числах начало зарождаться в 1545 году, когда итальянский математик, инженер, философ, медик и астролог Джироламо Кардано в своем трактате «Великое искусство» опубликовал данный метод решения уравнений, где, кстати, признался, что идею ему передал Никколо Тарталья (итальянский математик) за 6 лет до публикации этой работы. В работе Крадано решал уравнения вида:
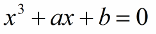
В процессе решения данных уравнений ученый вынужден был допустить существование некого «нереального» числа, квадрат которого был бы равен минус единице «-1», то есть будто бы существует квадратный корень из отрицательного числа, и если его теперь возвести в квадрат, то получится, соответственно, отрицательное число, стоящее под корнем. Кардано указал правило умножения, согласно которому:
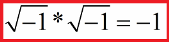
На протяжении трех веков математическое сообщество пребывало в процессе привыкания к новому подходу, предложенному Кардано. Мнимые числа постепенно приживались, однако принимались математиками неохотно. И лишь с публикациями работ Карла Фридриха Гаусса по алгебре, где он доказывал основную теорему алгебры, комплексные числа наконец-то основательно приняли, на дворе был 19 век.
Мнимые числа стали настоящей палочкой — выручалочкой для математиков, ведь сложнейшие задачи стали решаться гораздо проще с приятием существования мнимых чисел.
Так вскоре дело дошло и до электротехники. Электрические цепи переменного тока порой оказывались очень сложными, и для их расчета приходилось вычислять множество интегралов, что зачастую весьма неудобно.
Наконец, в 1893 году гениальный электротехник Карл Август (Чарлз Протеус) Штейнмец выступает в Чикаго на Международном электротехническом конгрессе с докладом «Комплексные числа и их применение в электротехнике», чем фактически знаменует начало практического применения инженерами комплексного метода расчетов электрических цепей переменного тока.
В своем докладе Штейнмец ввел понятие комплексной мощности, которая состоит из активной и реактивной составляющих, и показал, как можно вычислять их с помощью комплексных чисел. Он также разработал методы для анализа и синтеза полифазных систем, которые широко используются в электроэнергетике.
Доклад Штейнмеца произвел большое впечатление на электротехническое сообщество и стал поворотным моментом в развитии теории и практики переменного тока.
Благодаря комплексным числам, инженеры получили мощный инструмент для решения сложных задач, связанных с переменным током. Комплексные числа стали неотъемлемой частью электротехники и электроэнергетики.

Почему при расчетах переменных токов нельзя использовать те же формулы, что и при расчетах постоянных токов?
При расчетах переменных токов нельзя использовать те же формулы, что и при расчетах постоянных токов, потому что в цепях переменного тока возникают дополнительные эффекты, связанные с индуктивностью и ёмкостью элементов цепи. Эти эффекты приводят к тому, что сопротивление цепи зависит не только от ее активного сопротивления, но и от частоты переменного тока. Кроме того, в цепях переменного тока могут быть фазовые сдвиги между напряжением и током, которые также влияют на характеристики цепи.
Комплексные числа в расчетах переменных токов
Комплексные числа в электротехнике и электронике используются для упрощения расчетов переменных токов и напряжений, а также для анализа фазовых сдвигов, импедансов, резонансов и других явлений в электрических цепях.
Комплексные числа позволяют заменить графические методы решения задач на алгебраические, а также применять общие законы и формулы, которые справедливы для постоянного тока, к переменному току. Они также помогают моделировать различные физические процессы, такие как колебания и волны.
Для расчетов в цепях переменного тока комплексные числа используются, потому что они позволяют учесть фазовые сдвиги между напряжением и током в различных элементах цепи, таких как резисторы, конденсаторы и катушки индуктивности.
Для работы с комплексными числами в электротехнике нужно знать, как выполнять основные алгебраические операции над ними, такие, как сложение, вычитание, умножение и деление, а также как переводить их из алгебраической формы в тригонометрическую или показательную форму и обратно. Также полезно знать, как находить модуль и аргумент комплексного числа, которые соответствуют амплитуде и фазе переменной величины.
Из курса физики нам известно, что переменный ток — это такой ток, который изменяется во времени как по величине, так и по направлению.
В технике встречаются различные формы переменного тока, однако наиболее распространен сегодня ток переменный синусоидальный, именно такой используется всюду, при помощи его электроэнергия передается, в виде переменного тока она генерируется, преобразуется трансформаторами и потребляется нагрузками. Синусоидальный ток периодически изменяется по синусоидальному (гармоническому) закону.

Действующие значения тока и напряжения меньше амплитудных значений в корень из двух раз:
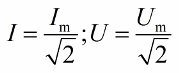
В комплексном методе действующие значения токов и напряжений записывают так:

Обратите внимание, что в электротехнике мнимая единица обозначается буквой «j», поскольку буква «i» уже занята здесь для обозначения тока.
Из закона Ома определяют комплексное значение сопротивления:

Сложение и вычитание комплексных значений осуществляется в алгебраической форме, а умножение и деление — в показательной форме.
Давайте разберем метод комплексных амплитуд на примере конкретной схемы с определенными значениями основных параметров.
Пример решения задачи с применением комплексных чисел
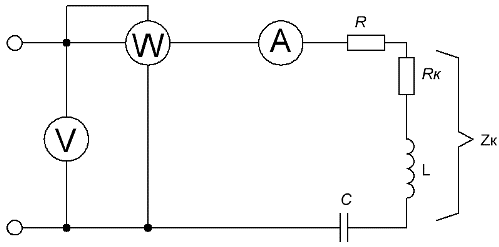
Дано:
-
напряжение на катушке 50 В,
-
сопротивление резистора 25 Ом,
-
индуктивность катушки 500 мГн,
-
электроемкость конденсатора 30 мкф,
-
сопротивление провода катушки 10 Ом,
-
частота сети 50 Гц.
Найти: показания амперметра и вольтметра, а также ваттметра.
Решение:
Для начала запишем комплексное сопротивление последовательно соединенных элементов, которое состоит из действительной и мнимой частей, затем найдем комплексное сопротивление активно-индуктивного элемента.
Вспоминаем! Для получения показательной формы находят модуль z, равный корню квадратному из суммы квадратов действительной и мнимой частей, а также фи, равное арктангенсу частного от деления мнимой части на действительную.
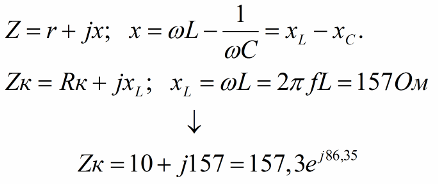
Далее найдем ток и соответственно показания амперметра:
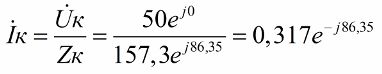
Итак, амперметр показывает ток 0,317 А — это ток через всю последовательную цепь.
Теперь найдем емкостное сопротивление конденсатора, затем определим его комплексное сопротивление:
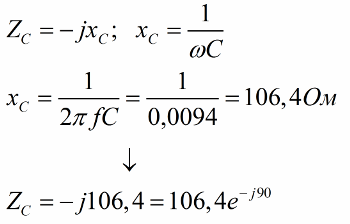
Далее вычислим полное комплексное сопротивление данной цепи:
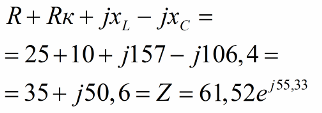
Теперь найдем действующее напряжение, приложенное к цепи:
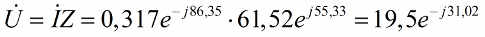
Вольтметр покажет действующее напряжение 19,5 вольт.
Наконец, найдем мощность, которую покажет ваттметр с учетом разности фаз между током и напряжением
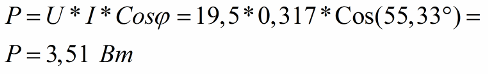
Ваттметр покажет 3,51 Ватт.
Теперь вы понимаете, какое важное место комплексные числа занимают в электротехнике. Они применяются для удобного расчета электрических цепей. На этой же основе работают и многие электронные измерительные приборы.
«
Подписывайтесь на наши каналы в Telegram:
Школа для электрика и Электрика, электромонтажные работы
Ответы на популярные вопросы по теме статьи
Вопрос: Почему в электротехнике используются комплексные числа, а не обычные?
Ответ: Комплексные числа позволяют описать одновременно два параметра электрической цепи — величину (амплитуду) и направление (фазу) переменного напряжения или тока. При расчётах постоянного тока достаточно одного числа, но в цепях переменного тока присутствуют сдвиги фаз между напряжением и током, которые невозможно описать обычными числами. Комплексные числа упрощают расчёты и позволяют использовать те же методы, что и для постоянного тока.
Вопрос: В чём разница между расчётом цепей постоянного и переменного тока?
Ответ: При расчётах постоянного тока достаточно знать только сопротивление элементов. В цепях переменного тока появляются дополнительные эффекты: индуктивное сопротивление (в катушках) и ёмкостное сопротивление (в конденсаторах). Кроме того, в переменном токе возникают сдвиги фаз между напряжением и током, что влияет на общую мощность, потребляемую цепью. Всё это нельзя учесть простыми числами.
Вопрос: Что такое мнимая единица в электротехнике и зачем она нужна?
Ответ: Мнимая единица в электротехнике обозначается буквой j (вместо i, которая зарезервирована для обозначения тока) и представляет поворот величины на 90 градусов. Например, если обычное число 5 описывает величину в одном направлении, то 5j описывает ту же величину, но сдвинутую на 90 градусов. Это позволяет описать реактивные составляющие цепи — индуктивное и ёмкостное сопротивления.
Вопрос: Кто первым предложил использовать комплексные числа в электротехнике?
Ответ: Идея мнимых чисел зародилась в 1545 году у итальянского математика Джироламо Кардано, когда он решал сложные уравнения. Однако в электротехнику комплексные числа применил гениальный электротехник Карл Август Штейнмец. В 1893 году он выступил с докладом на Международном электротехническом конгрессе в Чикаго, представив метод расчётов электрических цепей с использованием комплексных чисел. Этот доклад стал поворотным моментом в практическом применении этого метода.
Вопрос: Что такое активная и реактивная мощность?
Ответ: Активная мощность — это мощность, которая реально потребляется и преобразуется в тепло, свет или механическую работу (как в обычных резисторах). Реактивная мощность — это мощность, которая накапливается и отдаётся обратно в цепь без полезного преобразования энергии (происходит в катушках и конденсаторах). Комплексные числа помогают учесть обе эти составляющие одновременно и понять, сколько энергии действительно потребляется нагрузкой.
Вопрос: Можно ли использовать комплексные числа для анализа однофазных и трёхфазных цепей?
Ответ: Да, комплексные числа универсальны. Они работают как для однофазных цепей переменного тока (как в бытовых сетях), так и для трёхфазных систем (которые используются в промышленности). В трёхфазных системах комплексные числа становятся ещё более полезными, так как позволяют анализировать фазовые сдвиги между тремя фазами.
Вопрос: Какие операции с комплексными числами используют при расчётах электрических цепей?
Ответ: Используют четыре основные операции: сложение, вычитание, умножение и деление. При этом сложение и вычитание удобнее выполнять, когда число записано в алгебраической форме (с действительной и мнимой частями), а умножение и деление — когда число представлено в показательной форме (с модулем и аргументом, то есть величиной и углом сдвига фаз).
Вопрос: Что показывают приборы при измерении переменного тока в сложной цепи?
Ответ: Амперметр показывает действующее (эффективное) значение тока. Вольтметр показывает действующее напряжение. Ваттметр показывает активную мощность с учётом фазового сдвига между напряжением и током. Благодаря комплексным числам можно предсказать все эти значения, рассчитав цепь заранее, и понять, как изменения в цепи повлияют на показания приборов.
Вопрос: Почему математики в течение трёх веков неохотно принимали мнимые числа?
Ответ: Потому что мнимые числа казались "нереальными" и противоречили повседневному опыту. Невозможно иметь минус пять яблок, поэтому математики долго рассматривали комплексные числа как математический трюк, а не как реальный инструмент. Только в XIX веке, когда Карл Фридрих Гаусс доказал основную теорему алгебры и показал, что комплексные числа имеют глубокий математический смысл, они получили широкое признание.
Вопрос: Какие преимущества дал комплексный метод инженерам-электротехникам?
Ответ: До применения комплексных чисел инженеры вынуждены были решать сложные системы интегральных уравнений, что занимало много времени и было неудобно. Комплексный метод позволил заменить эти громоздкие вычисления простыми алгебраическими операциями. Это значительно ускорило расчёты, сделало их более надёжными и позволило анализировать сложные полифазные системы электроснабжения, которые сегодня используются по всему миру.
Вопрос: Почему буква j, а не i обозначает мнимую единицу в электротехнике?
Ответ: Потому что буква i в электротехнике уже зарезервирована для обозначения электрического тока. Чтобы не создавать путаницу и не спутать мнимую единицу с переменной величиной тока, в электротехнических расчётах приняли использовать букву j для обозначения мнимой единицы.
Андрей Повный


