Символический метод операций с векторными величинами основывается на весьма простой идее: каждый вектор раскладывают на две составляющие: одну — горизонтальную, идущую по оси абсцисс, а вторую — вертикальную, идущую по оси ординат. В этом случае все горизонтальные составляющие идут по одной прямой, и их можно складывать с помощью простого алгебраического сложения, аналогичным образом складывают и вертикальные составляющие.
Символический метод операций с векторными величинами основывается на весьма простой идее: каждый вектор раскладывают на две составляющие: одну — горизонтальную, идущую по оси абсцисс, а вторую — вертикальную, идущую по оси ординат. В этом случае все горизонтальные составляющие идут по одной прямой, и их можно складывать с помощью простого алгебраического сложения, аналогичным образом складывают и вертикальные составляющие.
При таком подходе в общем случае получаются две результирующие составляющие — горизонтальная и вертикальная, которые всегда находятся друг к другу под одним и тем же углом, равным 90°.
По этим составляющим можно найти их равнодействующую, т. е. произвести их геометрическое сложение. Составляющие под прямым углом представляют катеты прямоугольного треугольника, а их геометрическая сумма — гипотенузу.
Можно также сказать, что геометрическая сумма численно равна диагонали параллелограмма, построенного на составляющих, как на его сторонах. Если горизонтальную составляющую обозначить АГ а вертикальную — АВ, то геометрическая сумма (1)
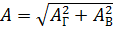
Находить геометрическую сумму прямоугольных треугольников гораздо легче, чем косоугольных. Легко видеть, что (2)
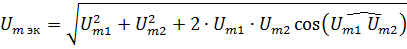
превращается в (1) если угол между составляющими составляет 90°. Поскольку cos 90 = 0, последний член в подкоренном выражении (2) исчезает, вследствие чего выражение резко упрощается. Обратим внимание на то, что перед словом "сумма" обязательно следует добавлять одно из трех слов: "арифметическая", "алгебраическая", "геометрическая".
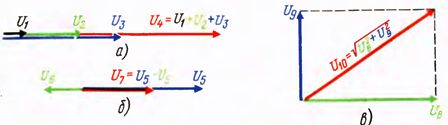
Рис.1.
Слово "сумма" без указания, какая именно, приводит к неопределенности, а в ряде случаев и к грубым ошибкам.
Напомним, что результирующий вектор равен арифметической сумме векторов в том случае, когда все векторы идут по одной прямой (или параллельно друг другу) в одинаковом направлении. При этом все векторы имеют знак плюс (рис. 1, а).
Если векторы идут по одной прямой, но направлены в противоположные стороны, то их равнодействующая равна алгебраической сумме векторов, в этом случае одни члены имеют знак плюс, а другие минус.
Например, в схеме рис. 1, б U6 = U4 — U5. Можно также сказать, что арифметическую сумму используют в тех случаях, когда угол между векторами равен нулю, алгебраическую, когда углы составляют 0 и 180°. Во всех остальных случаях сложение производят векторно, т. е. определяют геометрическую сумму (рис. 1, в).
«
Подписывайтесь на наши каналы в Telegram:
Школа для электрика и Электрика, электромонтажные работы
Пример. Определить параметры эквивалентной синусоиды для цепи рис. 2, а символическим методом.
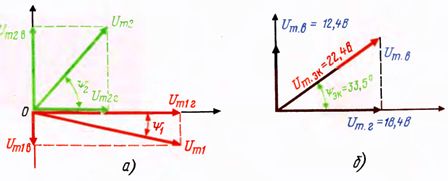
Решение. Нарисуем векторы Um1 Um2 и разложим их на составляющие. Из чертежа видно, что каждая горизонтальная составляющая представляет значение вектора, умноженное на косинус фазного угла, а вертикальная — значение вектора, умноженное на синус фазного угла. В данном случае
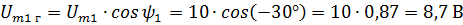
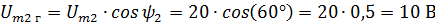
Рис.2.
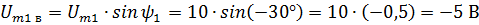
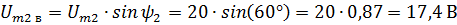
Очевидно, что общие горизонтальные и вертикальная составляющие равны алгебраическим суммам соответствующих составляющих. В данном случае
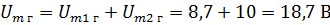
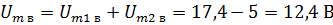
Получившиеся составляющие покажем на рис. 2, б. Определим значение Um для этого вычислим геометрическую сумму обеих составляющих:
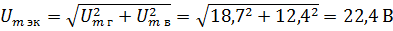
Определим эквивалентный фазный угол ψэк. Из рис. 2,б видно, что отношение вертикальной составляющей к горизонтальной представляет тангенс эквивалентного фазного угла.
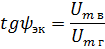
откуда
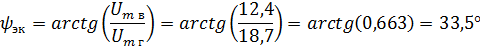
Таким образом, результирующая синусоида имеет амплитуду 22,4 В, начальную фазу 33,5° с таким же периодом, который имели составляющие. Заметим, что складывать можно только синусоиды с одинаковыми частотами поскольку при сложении синусоидальных кривых с различными частотами, результирующая кривая перестает быть синусоидальной и все понятия, приложимые только к гармоническим сигналам, становятся в этом случае неправомерными.
Проследим еще раз всю цепочку преобразований, которые приходится проделывать с математическими описаниями сигналов гармонической формы при выполнении различных расчетов.
Сначала временные функции заменяют векторными изображениями, затем каждый вектор раскладывают на две взаимно перпендикулярные составляющие, после чего просчитывают отдельно горизонтальные и вертикальные составляющие и, наконец, определяют значения результирующего вектора и его начальной фазы.
Такой путь расчета избавляет от необходимости графически складывать (а в ряде случаев делать и более сложные операции, например, перемножать делить, извлекать корни и т. д.) синусоидальные кривые и прибегать к расчетам с помощью формул косоугольных треугольников.
Однако рассчитывать отдельно горизонтальные и вертикальные составляющие операции достаточно громоздкие. При подобных расчетах очень удобным является такой математический аппарат, с помощью которого можно просчитать сразу обе составляющие.
Уже в конце прошлого века был разработан метод, позволяющий одновременно производить расчеты над числами, отложенными на взаимно перпендикулярных осях. Числа, откладываемые по горизонтальной оси, назвали вещественными, а по вертикальной оси — мнимыми. При расчетах этих чисел к вещественным добавляют множитель ± 1, а к мнимым — ±j (читается "жи"). Числа, состоящие из вещественной и мнимой частей, назвали комплексными, а метод расчетов, выполняемых с их помощью — символическим.
Поясним термин "символический". Те функции, которые подлежат расчету (в данном случае гармонические), являются оригиналами, а те выражения, которыми заменяют оригиналы — изображениями или символами.
При использовании символического метода все расчеты производят не над самими оригиналами, а над их символами (изображениями), которые в нашем случае представляют соответствующие комплексные числа, поскольку производить операции над изображениями значительно легче, чем над самими оригиналами.
По окончании всех операций над изображениями по результирующему изображению записывают оригинал, соответствующий получившемуся изображению. Символическим методом производят подавляющее большинство расчетов в электрических цепях.