Значимость электродинамики в современном мире связана прежде всего с широкими техническими возможностями, которые она открывает для передачи электрической энергии по проводам на большие расстояния, для способов распределения и преобразования электричества в другие формы, - в механическую, тепловую, световую и т. д.
Генерируемая на электростанциях, электрическая энергия отправляется через многие километры по линиям электропередачи — в дома и на промышленные объекты, где электромагнитные силы приводят в действие двигатели различного оборудования, бытовую технику, осветительные, нагревательные приборы и прочее. Словом, без розетки на стене невозможно представить ни одно современное хозяйство и ни одно помещение.
Все это стало когда-то возможным только благодаря знаниям законов электродинамики, позволяющих связать теорию с практическим применением электричества. В данной статье мы подробно рассмотрим четыре наиболее практически важных из этих законов.
Закон электромагнитной индукции
На законе электромагнитной индукции основана работа всех электрогенераторов, установленных на электростанциях и не только. А ведь все началось с едва заметного тока, обнаруженного в 1831 году Майклом Фарадеем в эксперименте с перемещением электромагнита относительно катушки.
Когда Фарадея спросили о перспективах его открытия, он сравнил результат своего эксперимента с рождением ребенка, которому еще только предстояло повзрослеть. Вскоре этот новорожденный превратился в настоящего богатыря, изменившего облик всего цивилизованного мира. Смотрите - Практическое применение закон электромагнитной индукции
Генератор на истоической гидроэлектростанции в Германии
Современный генератор электростанции представляет собой не просто катушку с магнитом. Это огромное сооружение, содержащее стальные конструкции, множество катушек из изолированных друг от друга медных шин, тонны железа, изоляционные материалы, а также большое количество мелких деталей, изготовленных с точностью до долей миллиметра.
В природе такого сложного устройства, конечно, не встретить, однако именно природа в эксперименте показала человеку то, как должен работать прибор для производства электричества посредством механических перемещений под действием доступной внешней силы.
Генерируемое на электростанции электричество преобразуется, распределяется и снова преобразуется благодаря силовым трансформаторам, работа которых тоже основывается на явлении электромагнитной индукции, только трансформатор, в отличие от генератора, не включает в свою конструкцию постоянно движущихся частей, вместо этого он содержит магнитопровод с катушками.
Одна катушка с переменным током (первичная катушка) действует на магнитопровод, магнитопровод действует на вторичные катушки (вторичные обмотки трансформатора). Электричество со вторичных обмоток трансформатора уже распределяется к потребителям. Все это работает благодаря явлению электромагнитной индукции и знанию соответствующего закона электродинамики, носящего имя Фарадея.
Физический смысл закона электромагнитной индукции заключается в возникновении вихревого электрического поля при изменении во времени магнитного поля, что как раз и происходит в работающем трансформаторе.
Практически, когда изменяется магнитный поток, пронизывающий ограниченную проводником поверхность, в проводнике наводится ЭДС, величина которой равна скорости изменения магнитного потока (Ф), при этом знак наводимой ЭДС противоположен скорости производимого изменения Ф. Данное соотношение называют еще «правилом потока»:
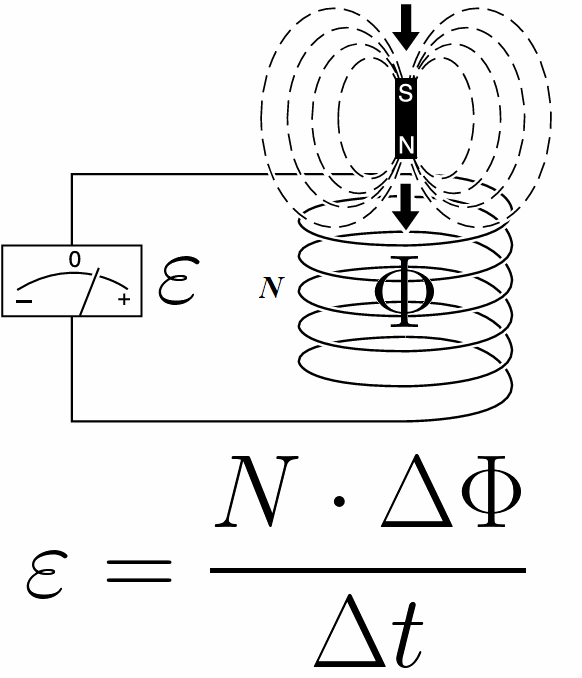
Кроме непосредственного изменения пронизывающего контур магнитного потока, возможен и другой способ получения в нем ЭДС, - с помощью силы Лоренца.
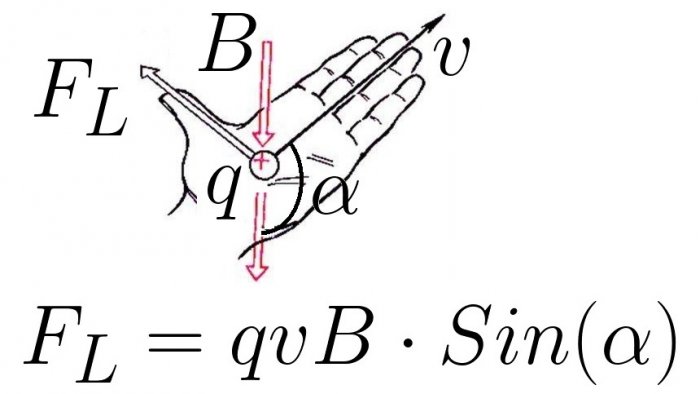
Величина силы Лоренца зависит, как известно, от скорости движения заряда в магнитном поле, от величины индукции магнитного поля, и от угла, под которым данный заряд движется относительно вектора индукции магнитного поля:
Направление силы Лоренца для положительного заряда определяется правилом «левой руки»: если расположить левую руку так, чтобы вектор магнитной индукции входил в ладонь, а четыре вытянутых пальца расположить по направлению движения положительного заряда, то отогнутый на 90 градусов большой палец покажет направление силы Лоренца.
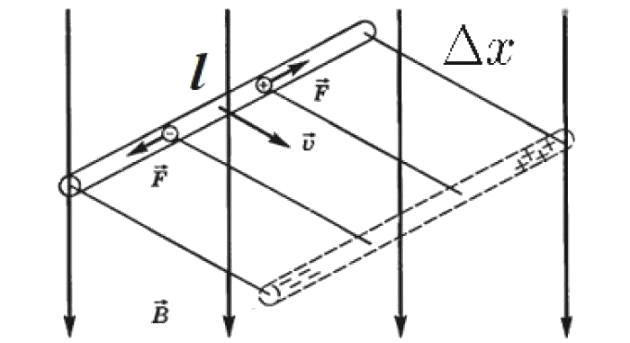
Простейший пример такого случая представлен на рисунке. Здесь сила Лоренца заставляет верхний конец движущегося в магнитном поле проводника (допустим — куска медной проволоки) зарядиться положительно, а нижний его конец — отрицательно, поскольку электроны имеют отрицательный заряд и именно они движутся здесь вниз.
Электроны будут двигаться вниз до тех пор, пока сила кулоновского притяжения между ними и положительным зарядом с противоположной стороны провода не уравновесит силу Лоренца.
Данный процесс обуславливает возникновение ЭДС индукции в проводнике, и, как выяснилось, имеет прямое отношение к закону электромагнитной индукции. В самом деле, напряженность электрического поля Е в проводнике можно найти следующим образом (примем, что проводник движется под прямым углом к вектору B):
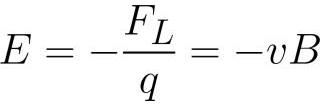
следовательно ЭДС индукции может быть выражена так:
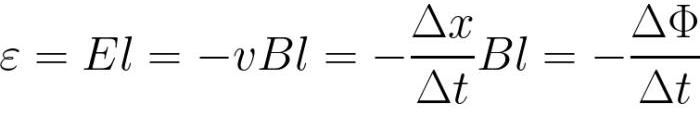
Можно заметить, что в приведенном примере непосредственно магнитный поток Ф (как объект) не претерпевает изменений в пространстве, зато происходит пересечение проводником области, в которой присутствует магнитный поток, и можно легко вычислить площадь, которую проходит проводник, двигаясь через данную область пространства в течение заданного времени (то есть упомянутую ранее скорость изменения магнитного потока).
«
Подписывайтесь на наши каналы в Telegram:
Школа для электрика и Электрика, электромонтажные работы
В общем случае имеем право заключить, что, согласно «правилу потока», ЭДС в контуре равна взятой с обратным знаком скорости изменения магнитного потока через данный контур независимо от того, меняется ли величина непосредственно потока Ф из-за изменения индукции магнитного поля во времени при неподвижном контуре, или же в результате перемещения (пересечения магнитного потока) или деформации контура, либо из-за того и другого вместе.
Закон Ампера
Значительная часть генерируемой на электростанциях энергии направляется на предприятия, где электричеством питаются двигатели разнообразных станков. Действие электродвигателей основано на понимании их проектировщиками закона Ампера.
Данный закон Андре Мари Ампер установил в 1820 году для постоянных токов (не даром этот закон называют еще законом взаимодействия электрических токов).
Согласно закону Ампера, параллельные проводники с токами одного направления взаимно притягиваются, а параллельные проводники с противоположно направленными токами друг друга отталкивают. Кроме того, законом Ампера именуется фундаментальное правило определения силы, с которой магнитное поле действует на проводник с током, находящийся в данном поле.
В простом виде закон Ампера можно сформулировать так: сила (называемая силой Ампера), с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна величине тока в проводнике и векторному произведению элемента длины проводника на значение магнитной индукции.
Соответственно, выражение для нахождения модуля силы Ампера содержит синус угла между вектором магнитной индукции и вектором тока в проводнике, на который действует данная сила (для определения направления силы Ампера можно пользоваться правилом левой руки):
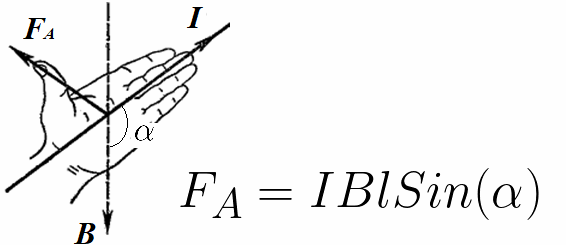
Применительно к двум взаимодействующим проводникам, сила Ампера будет действовать на каждый из них в направлении, зависящем от соответствующих направлений токов в данных проводниках.
Допустим, в вакууме расположены два бесконечно длинных тонких проводника с токами I1 и I2, а расстояние между проводниками всюду равно r. Необходимо найти силу Ампера, действующую на единицу длины проводника (допустим, на первый проводник со стороны второго).
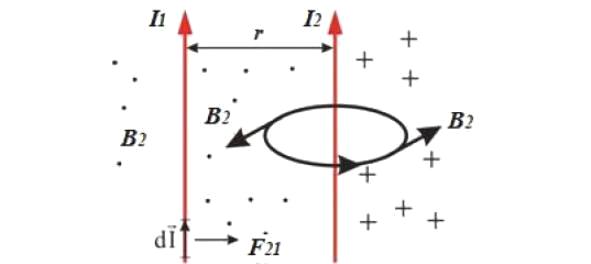
По закону Био-Савара-Лапласа, на расстоянии r от бесконечного проводника с током I2, магнитное поле будет иметь индукцию:
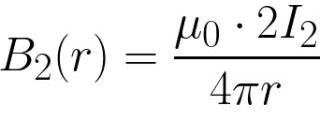
Теперь можно найти и силу Ампера, которая будет действовать на первый проводник, находящийся в данной точке магнитного поля (в месте с данной индукцией):
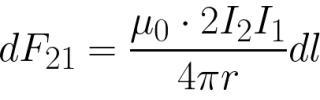
Проинтегрировав данное выражение по длине, а затем подставив в качестве длины единицу, получим силу Ампера, действующую на единицу длины первого проводника со стороны второго. Аналогичная сила, только противоположно направленная, будет действовать на второй проводник со стороны первого.
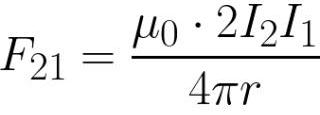
Без понимания закона Ампера было бы попросту невозможно качественно спроектировать и собрать хоть один нормальный электродвигатель.
Принцип действия и устроство электродвигателя
Типы асинхронных электродвиагетелей, их особенности
Закон Джоуля-Ленца
Вся электрическая энергия, передаваемая по линиям электропередачи, вызывает нагрев данных проводников. Кроме того немалые электрические мощности используются по назначению для питания различных нагревательных приборов, для накала вольфрамовых нитей до высоких температур и т. д. Расчеты теплового действия электрического тока базируются на законе Джоуля-Ленца, открытом в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем.
Данный закон дает количественную оценку теплового действия электрического тока. Формулируется он так: «Мощность тепла, выделяемого в единице объема (w) среды при протекании в ней постоянного электрического тока, пропорциональна произведению плотности электрического тока (j) на величину напряженности электрического поля (E)».
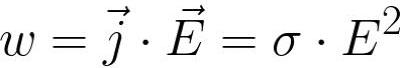
Для тонких проводников применяют интегральную форму закона: «количество теплоты, выделяемое за единицу времени участком цепи, пропорционально произведению квадрата величины тока на рассматриваемом участке на сопротивление участка». Записывается в следующем виде:
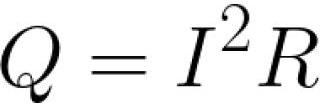
Закон Джоуля-Ленца приобретает особенно важное практическое значение при передаче электрической энергии по проводам на большие расстояния.
Суть в том, что тепловое действие тока на ЛЭП является нежелательным, так как ведет к потерям энергии. А поскольку передаваемая мощность линейно зависит как от напряжения, так и от величины тока, тогда как мощность нагрева пропорциональна квадрату тока, то выгодно повышать напряжение при котором передается электроэнергия, понижая соответственно ток.
Закон Ома
Основной закон электрической цепи — Закон Ома, открытый Георгом Омом в 1826 году. Закон определяет связь между электрическим напряжением и током в зависимости от электрического сопротивления или проводимости (электропроводности) проводника. В современных терминах закон Ома для полной цепи записывается так:
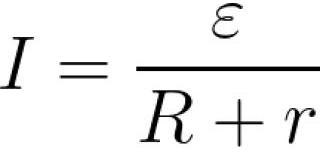
r – внутреннее сопротивление источника, R – сопротивление нагрузки, e – ЭДС источника, I – ток в цепи
Из данной записи следует, что ЭДС в замкнутой цепи, по которой течет даваемый источником ток, будет равна:
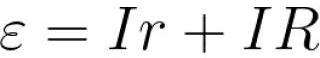
Это значит, что для замкнутой цепи ЭДС источника равна сумме падений напряжений на внешней цепи и на внутреннем сопротивлении источника.
Формулируется закон Ома так: «ток в участке цепи прямо пропорционален напряжению на его концах и обратно пропорционален электрическому сопротивлению данного участка цепи». Другая запись закона Ома — через проводимость G (электропроводность):
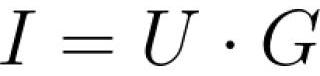
Применение закона Ома на практике
Что такое напряжение, ток, сопротивление и как они используются на практике